Parzen Window Approximation on Riemannian Manifold
Paper and Code
Dec 29, 2020

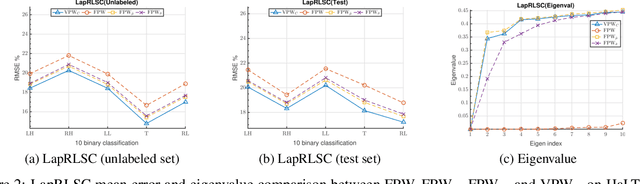
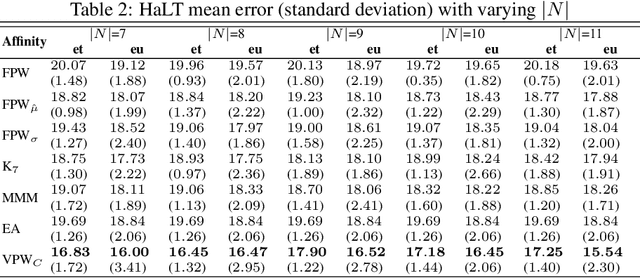
In graph motivated learning, label propagation largely depends on data affinity represented as edges between connected data points. The affinity assignment implicitly assumes even distribution of data on the manifold. This assumption may not hold and may lead to inaccurate metric assignment due to drift towards high-density regions. The drift affected heat kernel based affinity with a globally fixed Parzen window either discards genuine neighbors or forces distant data points to become a member of the neighborhood. This yields a biased affinity matrix. In this paper, the bias due to uneven data sampling on the Riemannian manifold is catered to by a variable Parzen window determined as a function of neighborhood size, ambient dimension, flatness range, etc. Additionally, affinity adjustment is used which offsets the effect of uneven sampling responsible for the bias. An affinity metric which takes into consideration the irregular sampling effect to yield accurate label propagation is proposed. Extensive experiments on synthetic and real-world data sets confirm that the proposed method increases the classification accuracy significantly and outperforms existing Parzen window estimators in graph Laplacian manifold regularization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge