Partitioning Strategies and Task Allocation for Target-tracking with Multiple Guards in Polygonal Environments
Paper and Code
Nov 15, 2016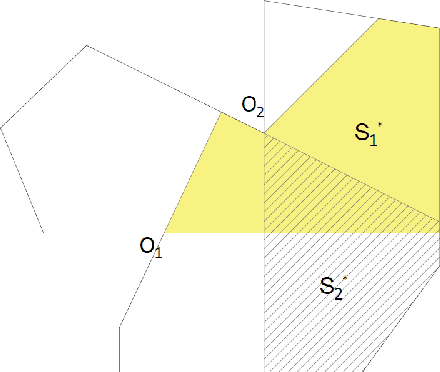
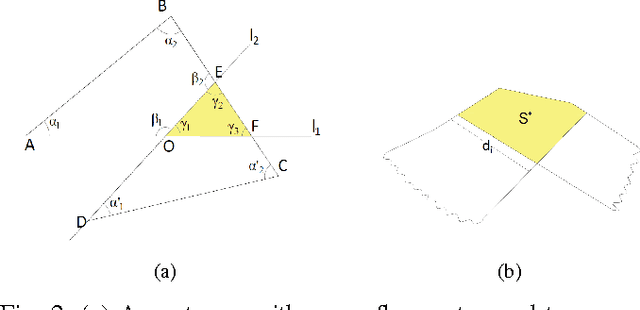
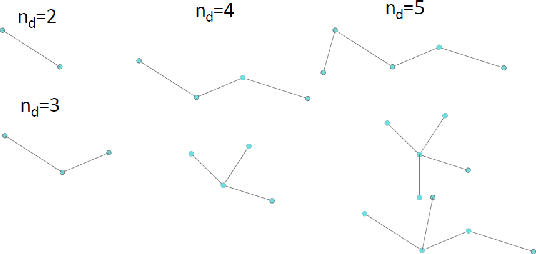
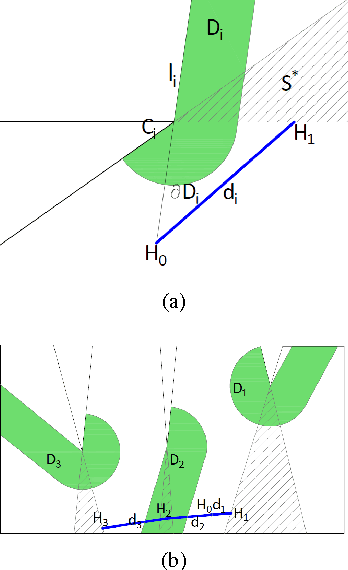
This paper presents an algorithm to deploy a team of {\it free} guards equipped with omni-directional cameras for tracking a bounded speed intruder inside a simply-connected polygonal environment. The proposed algorithm partitions the environment into smaller polygons, and assigns a guard to each partition so that the intruder is visible to at least one guard at all times. Based on the concept of {\it dynamic zones} introduced in this paper, we propose event-triggered strategies for the guards to track the intruder. We show that the number of guards deployed by the algorithm for tracking is strictly less than $\lfloor {\frac{n}{3}} \rfloor$ which is sufficient and sometimes necessary for coverage. We derive an upper bound on the speed of the mobile guard required for successful tracking which depends on the intruder's speed, the road map of the mobile guards, and geometry of the environment. Finally, we extend the aforementioned analysis to orthogonal polygons, and show that the upper bound on the number of guards deployed for tracking is strictly less than $\lfloor {\frac{n}{4}} \rfloor$ which is sufficient and sometimes necessary for the coverage problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge