Particle Metropolis adjusted Langevin algorithms for state space models
Paper and Code
Dec 24, 2014
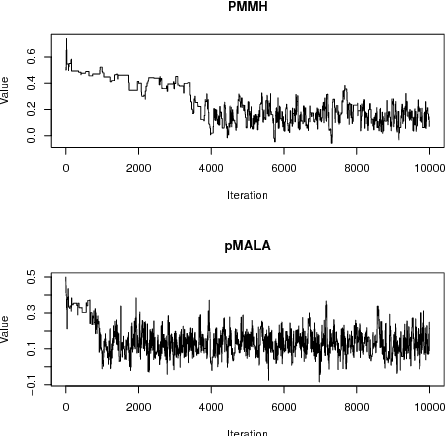
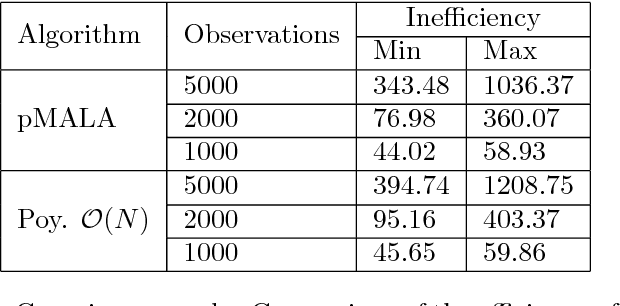
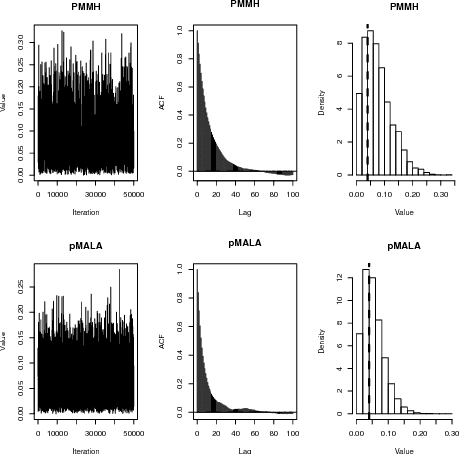
Particle MCMC is a class of algorithms that can be used to analyse state-space models. They use MCMC moves to update the parameters of the models, and particle filters to propose values for the path of the state-space model. Currently the default is to use random walk Metropolis to update the parameter values. We show that it is possible to use information from the output of the particle filter to obtain better proposal distributions for the parameters. In particular it is possible to obtain estimates of the gradient of the log posterior from each run of the particle filter, and use these estimates within a Langevin-type proposal. We propose using the recent computationally efficient approach of Nemeth et al. (2013) for obtaining such estimates. We show empirically that for a variety of state-space models this proposal is more efficient than the standard random walk Metropolis proposal in terms of: reducing autocorrelation of the posterior samples, reducing the burn-in time of the MCMC sampler and increasing the squared jump distance between posterior samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge