Particle Flow Gaussian Particle Filter
Paper and Code
Jul 04, 2022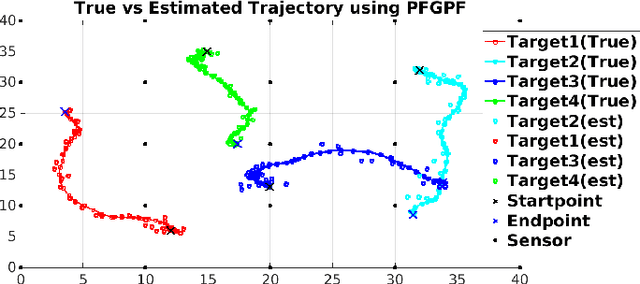
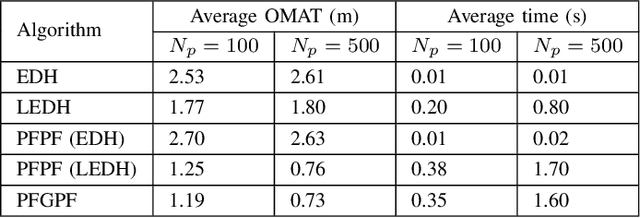
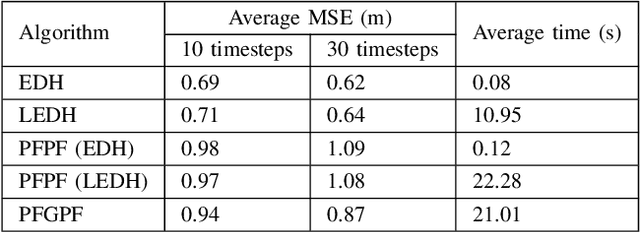
State estimation in non-linear models is performed by tracking the posterior distribution recursively. A plethora of algorithms have been proposed for this task. Among them, the Gaussian particle filter uses a weighted set of particles to construct a Gaussian approximation to the posterior. In this paper, we propose to use invertible particle flow methods, derived under the Gaussian boundary conditions for a flow equation, to generate a proposal distribution close to the posterior. The resultant particle flow Gaussian particle filter (PFGPF) algorithm retains the asymptotic properties of Gaussian particle filters, with the potential for improved state estimation performance in high dimensional spaces. We compare the performance of PFGPF with the particle flow filters and particle flow particle filters in two challenging numerical simulation examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge