Particle Dynamics for Learning EBMs
Paper and Code
Nov 26, 2021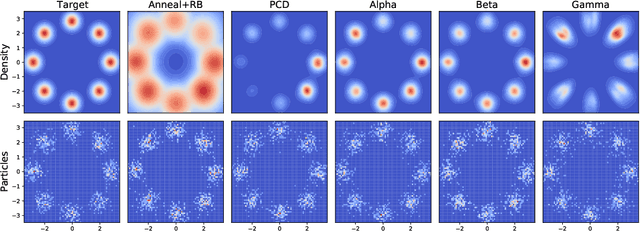
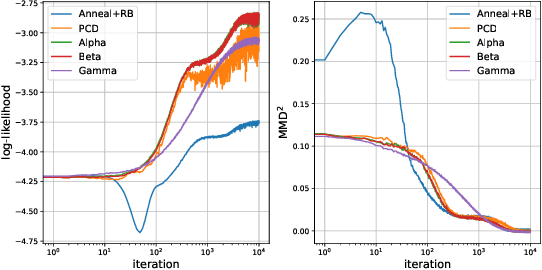
Energy-based modeling is a promising approach to unsupervised learning, which yields many downstream applications from a single model. The main difficulty in learning energy-based models with the "contrastive approaches" is the generation of samples from the current energy function at each iteration. Many advances have been made to accomplish this subroutine cheaply. Nevertheless, all such sampling paradigms run MCMC targeting the current model, which requires infinitely long chains to generate samples from the true energy distribution and is problematic in practice. This paper proposes an alternative approach to getting these samples and avoiding crude MCMC sampling from the current model. We accomplish this by viewing the evolution of the modeling distribution as (i) the evolution of the energy function, and (ii) the evolution of the samples from this distribution along some vector field. We subsequently derive this time-dependent vector field such that the particles following this field are approximately distributed as the current density model. Thereby we match the evolution of the particles with the evolution of the energy function prescribed by the learning procedure. Importantly, unlike Monte Carlo sampling, our method targets to match the current distribution in a finite time. Finally, we demonstrate its effectiveness empirically compared to MCMC-based learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge