Particle Dual Averaging: Optimization of Mean Field Neural Networks with Global Convergence Rate Analysis
Paper and Code
Dec 31, 2020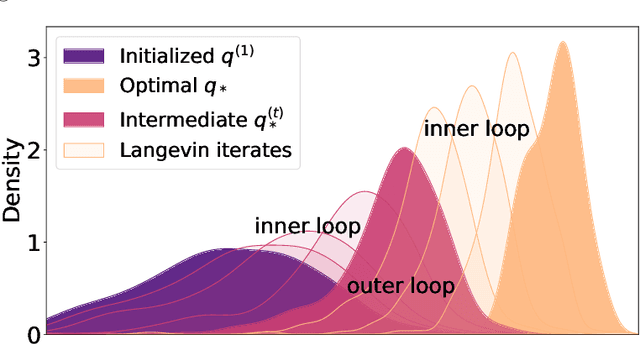
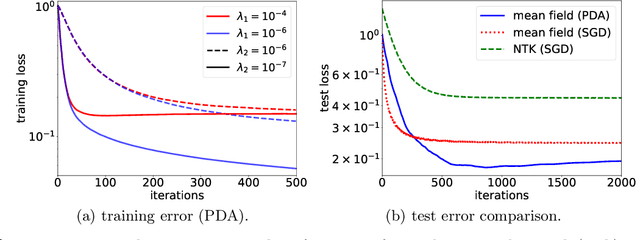
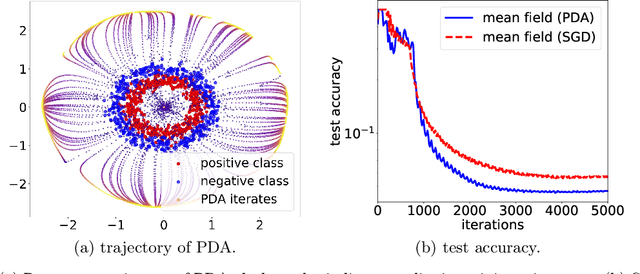
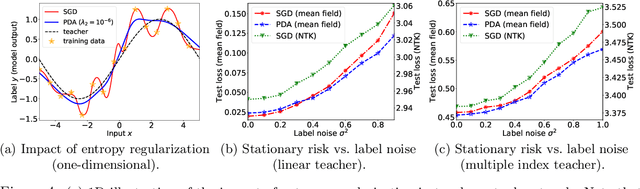
We propose the particle dual averaging (PDA) method, which generalizes the dual averaging method in convex optimization to the optimization over probability distributions with quantitative runtime guarantee. The algorithm consists of an inner loop and outer loop: the inner loop utilizes the Langevin algorithm to approximately solve for a stationary distribution, which is then optimized in the outer loop. The method can thus be interpreted as an extension of the Langevin algorithm to naturally handle nonlinear functional on the probability space. An important application of the proposed method is the optimization of two-layer neural network in the mean field regime, which is theoretically attractive due to the presence of nonlinear feature learning, but quantitative convergence rate can be challenging to establish. We show that neural networks in the mean field limit can be globally optimized by PDA. Furthermore, we characterize the convergence rate by leveraging convex optimization theory in finite-dimensional spaces. Our theoretical results are supported by numerical simulations on neural networks with reasonable size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge