Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

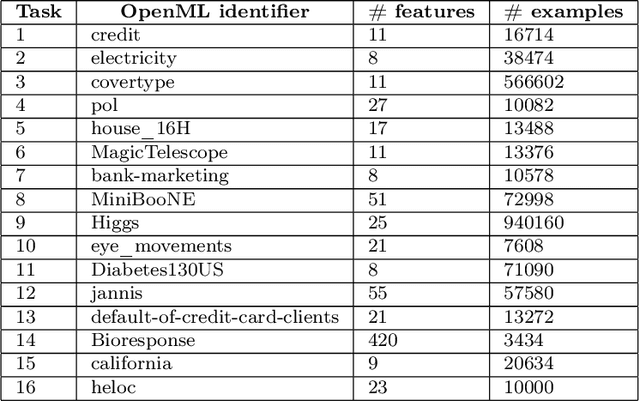
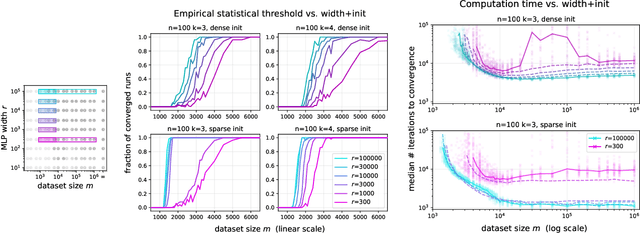
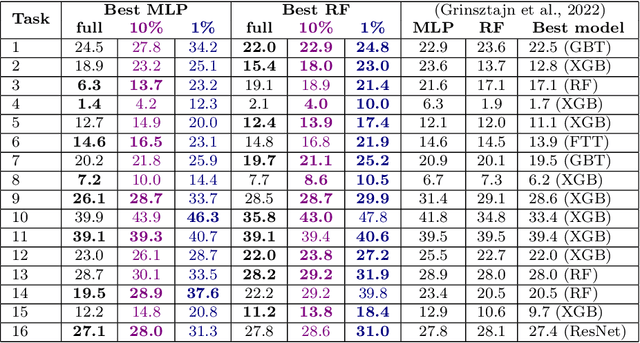
This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.