Parametric Dependability Analysis through Probabilistic Horn Abduction
Paper and Code
Oct 19, 2012
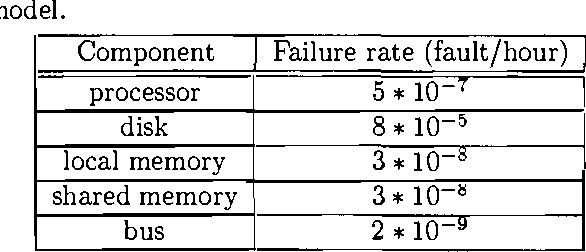
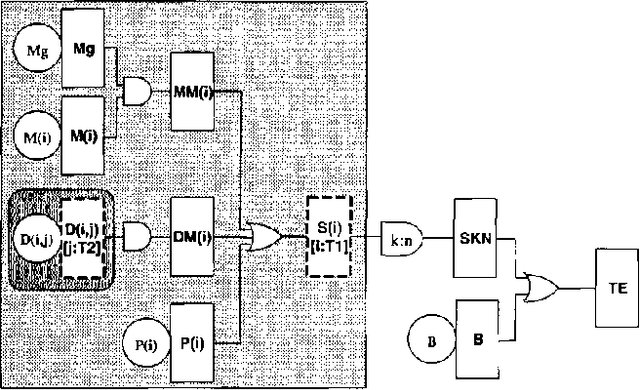
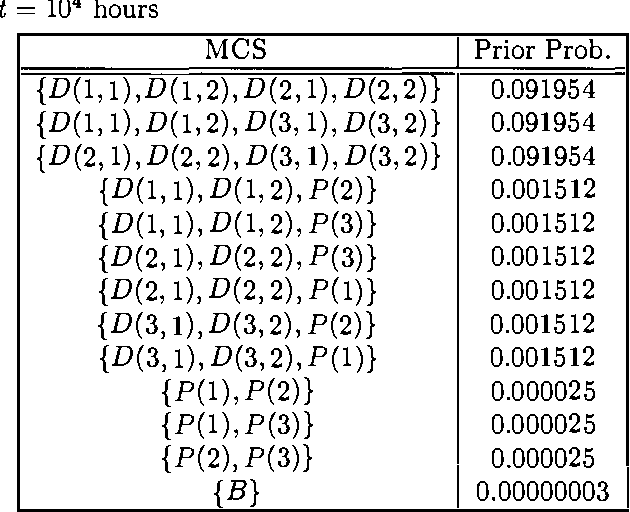
Dependability modeling and evaluation is aimed at investigating that a system performs its function correctly in time. A usual way to achieve a high reliability, is to design redundant systems that contain several replicas of the same subsystem or component. State space methods for dependability analysis may suffer of the state space explosion problem in such a kind of situation. Combinatorial models, on the other hand, require the simplified assumption of statistical independence; however, in case of redundant systems, this does not guarantee a reduced number of modeled elements. In order to provide a more compact system representation, parametric system modeling has been investigated in the literature, in such a way that a set of replicas of a given subsystem is parameterized so that only one representative instance is explicitly included. While modeling aspects can be suitably addressed by these approaches, analytical tools working on parametric characterizations are often more difficult to be defined and the standard approach is to 'unfold' the parametric model, in order to exploit standard analysis algorithms working at the unfolded 'ground' level. Moreover, parameterized combinatorial methods still require the statistical independence assumption. In the present paper we consider the formalism of Parametric Fault Tree (PFT) and we show how it can be related to Probabilistic Horn Abduction (PHA). Since PHA is a framework where both modeling and analysis can be performed in a restricted first-order language, we aim at showing that converting a PFT into a PHA knowledge base will allow an approach to dependability analysis directly exploiting parametric representation. We will show that classical qualitative and quantitative dependability measures can be characterized within PHA. Furthermore, additional modeling aspects (such as noisy gates and local dependencies) as well as additional reliability measures (such as posterior probability analysis) can be naturally addressed by this conversion. A simple example of a multi-processor system with several replicated units is used to illustrate the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge