Parametric and Multivariate Uncertainty Calibration for Regression and Object Detection
Paper and Code
Jul 04, 2022
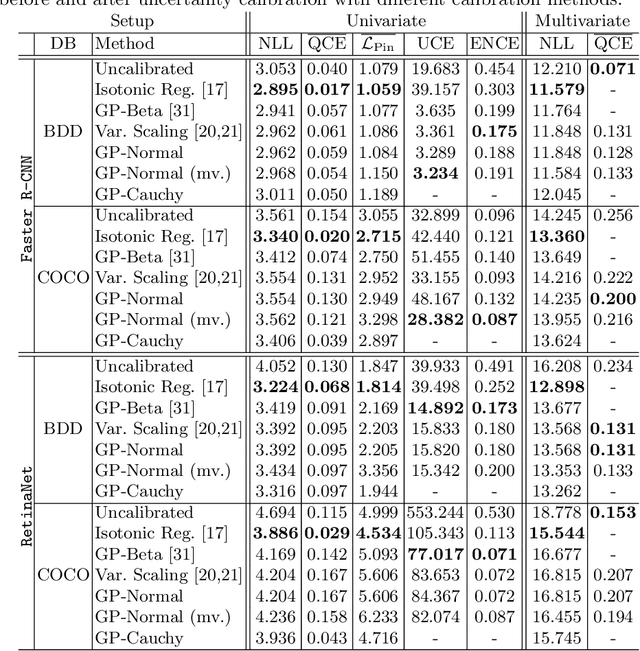
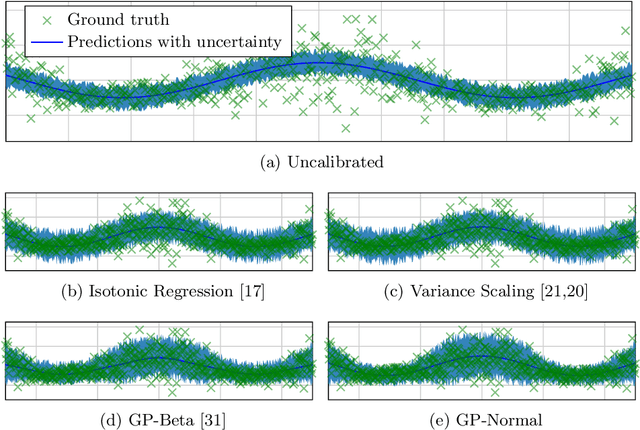
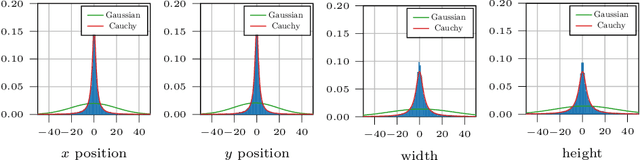
Reliable spatial uncertainty evaluation of object detection models is of special interest and has been subject of recent work. In this work, we review the existing definitions for uncertainty calibration of probabilistic regression tasks. We inspect the calibration properties of common detection networks and extend state-of-the-art recalibration methods. Our methods use a Gaussian process (GP) recalibration scheme that yields parametric distributions as output (e.g. Gaussian or Cauchy). The usage of GP recalibration allows for a local (conditional) uncertainty calibration by capturing dependencies between neighboring samples. The use of parametric distributions such as as Gaussian allows for a simplified adaption of calibration in subsequent processes, e.g., for Kalman filtering in the scope of object tracking. In addition, we use the GP recalibration scheme to perform covariance estimation which allows for post-hoc introduction of local correlations between the output quantities, e.g., position, width, or height in object detection. To measure the joint calibration of multivariate and possibly correlated data, we introduce the quantile calibration error which is based on the Mahalanobis distance between the predicted distribution and the ground truth to determine whether the ground truth is within a predicted quantile. Our experiments show that common detection models overestimate the spatial uncertainty in comparison to the observed error. We show that the simple Isotonic Regression recalibration method is sufficient to achieve a good uncertainty quantification in terms of calibrated quantiles. In contrast, if normal distributions are required for subsequent processes, our GP-Normal recalibration method yields the best results. Finally, we show that our covariance estimation method is able to achieve best calibration results for joint multivariate calibration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge