Parameter and Feature Selection in Stochastic Linear Bandits

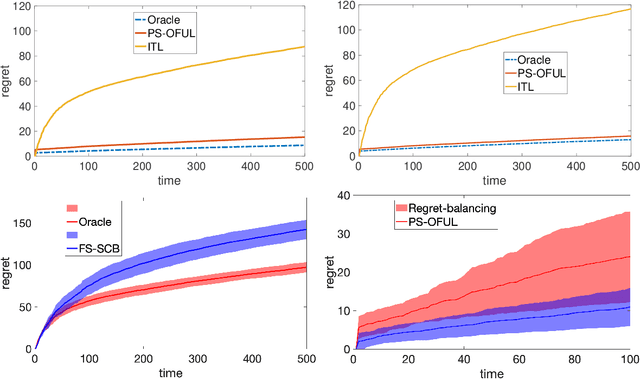
We study two model selection settings in stochastic linear bandits (LB). In the first setting, the reward parameter of the LB problem is arbitrarily selected from $M$ models represented as (possibly) overlapping balls in $\mathbb R^d$. However, the agent only has access to misspecified models, i.e., estimates of the centers and radii of the balls. We refer to this setting as parameter selection. In the second setting, which we refer to as feature selection, the expected reward of the LB problem is in the linear span of at least one of $M$ feature maps (models). For each setting, we develop and analyze an algorithm that is based on a reduction from bandits to full-information problems. This allows us to obtain regret bounds that are not worse (up to a $\sqrt{\log M}$ factor) than the case where the true model is known. Our parameter selection algorithm is OFUL-style and the one for feature selection is based on the SquareCB algorithm. We also show that the regret of our parameter selection algorithm scales logarithmically with model misspecification.