$ω$PAP Spaces: Reasoning Denotationally About Higher-Order, Recursive Probabilistic and Differentiable Programs
Paper and Code
Feb 21, 2023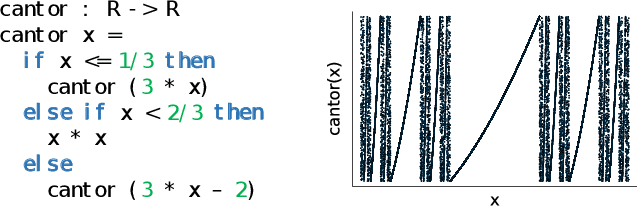


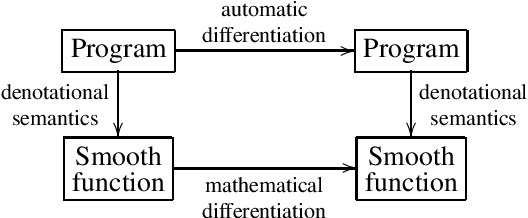
We introduce a new setting, the category of $\omega$PAP spaces, for reasoning denotationally about expressive differentiable and probabilistic programming languages. Our semantics is general enough to assign meanings to most practical probabilistic and differentiable programs, including those that use general recursion, higher-order functions, discontinuous primitives, and both discrete and continuous sampling. But crucially, it is also specific enough to exclude many pathological denotations, enabling us to establish new results about both deterministic differentiable programs and probabilistic programs. In the deterministic setting, we prove very general correctness theorems for automatic differentiation and its use within gradient descent. In the probabilistic setting, we establish the almost-everywhere differentiability of probabilistic programs' trace density functions, and the existence of convenient base measures for density computation in Monte Carlo inference. In some cases these results were previously known, but required detailed proofs with an operational flavor; by contrast, all our proofs work directly with programs' denotations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge