PAMELI: A Meta-Algorithm for Computationally Expensive Multi-Objective Optimization Problems
Paper and Code
Mar 19, 2021
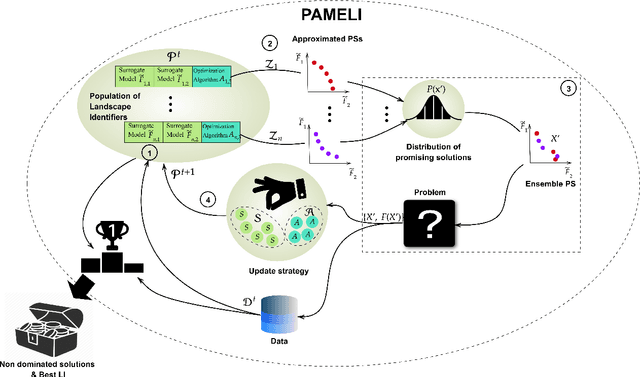
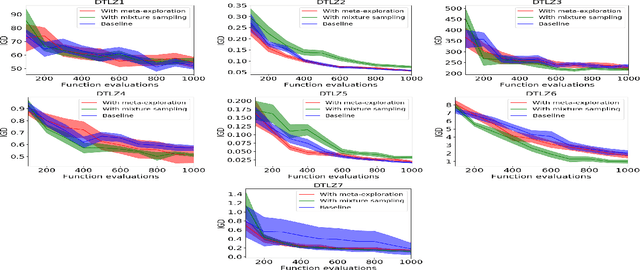
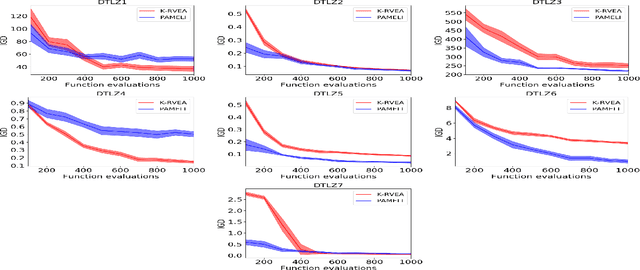
We present an algorithm for multi-objective optimization of computationally expensive problems. The proposed algorithm is based on solving a set of surrogate problems defined by models of the real one, so that only solutions estimated to be approximately Pareto-optimal are evaluated using the real expensive functions. Aside of the search for solutions, our algorithm also performs a meta-search for optimal surrogate models and navigation strategies for the optimization landscape, therefore adapting the search strategy for solutions to the problem as new information about it is obtained. The competitiveness of our approach is demonstrated by an experimental comparison with one state-of-the-art surrogate-assisted evolutionary algorithm on a set of benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge