P-split formulations: A class of intermediate formulations between big-M and convex hull for disjunctive constraints
Paper and Code
Feb 10, 2022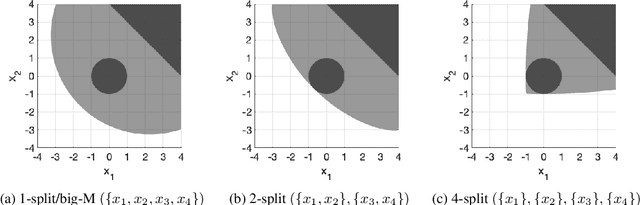
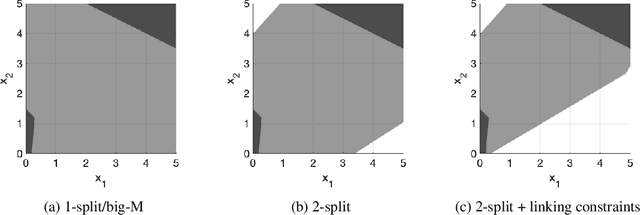
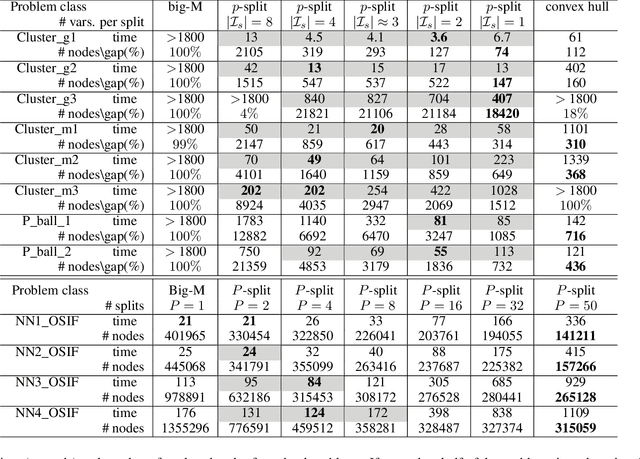
We develop a class of mixed-integer formulations for disjunctive constraints intermediate to the big-M and convex hull formulations in terms of relaxation strength. The main idea is to capture the best of both the big-M and convex hull formulations: a computationally light formulation with a tight relaxation. The "$P$-split" formulations are based on a lifted transformation that splits convex additively separable constraints into $P$ partitions and forms the convex hull of the linearized and partitioned disjunction. We analyze the continuous relaxation of the $P$-split formulations and show that, under certain assumptions, the formulations form a hierarchy starting from a big-M equivalent and converging to the convex hull. The goal of the $P$-split formulations is to form a strong approximation of the convex hull through a computationally simpler formulation. We computationally compare the $P$-split formulations against big-M and convex hull formulations on 320 test instances. The test problems include K-means clustering, P_ball problems, and optimization over trained ReLU neural networks. The computational results show promising potential of the $P$-split formulations. For many of the test problems, $P$-split formulations are solved with a similar number of explored nodes as the convex hull formulation, while reducing the solution time by an order of magnitude and outperforming big-M both in time and number of explored nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge