OTW: Optimal Transport Warping for Time Series
Paper and Code
Jun 01, 2023
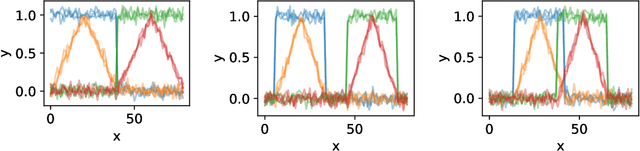
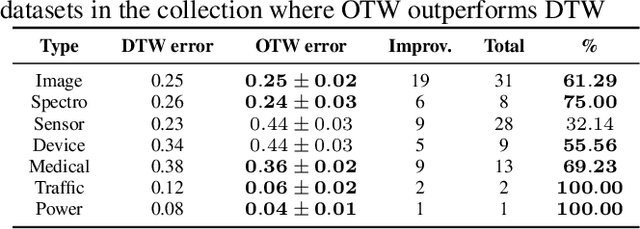
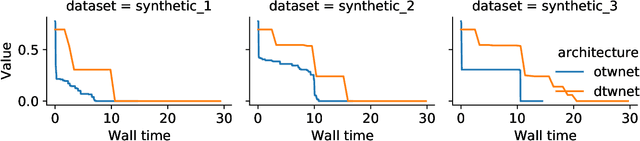
Dynamic Time Warping (DTW) has become the pragmatic choice for measuring distance between time series. However, it suffers from unavoidable quadratic time complexity when the optimal alignment matrix needs to be computed exactly. This hinders its use in deep learning architectures, where layers involving DTW computations cause severe bottlenecks. To alleviate these issues, we introduce a new metric for time series data based on the Optimal Transport (OT) framework, called Optimal Transport Warping (OTW). OTW enjoys linear time/space complexity, is differentiable and can be parallelized. OTW enjoys a moderate sensitivity to time and shape distortions, making it ideal for time series. We show the efficacy and efficiency of OTW on 1-Nearest Neighbor Classification and Hierarchical Clustering, as well as in the case of using OTW instead of DTW in Deep Learning architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge