Orthogonal Time Frequency Space Modulation: A Discrete Zak Transform Approach
Paper and Code
Jun 24, 2021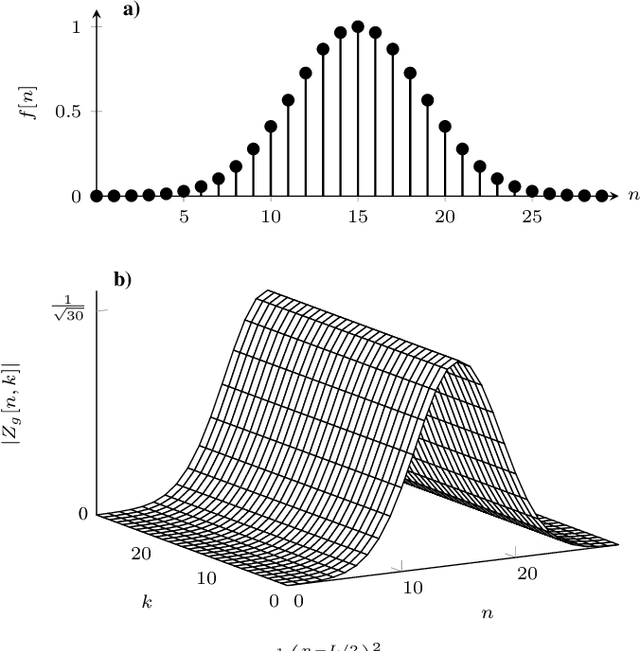

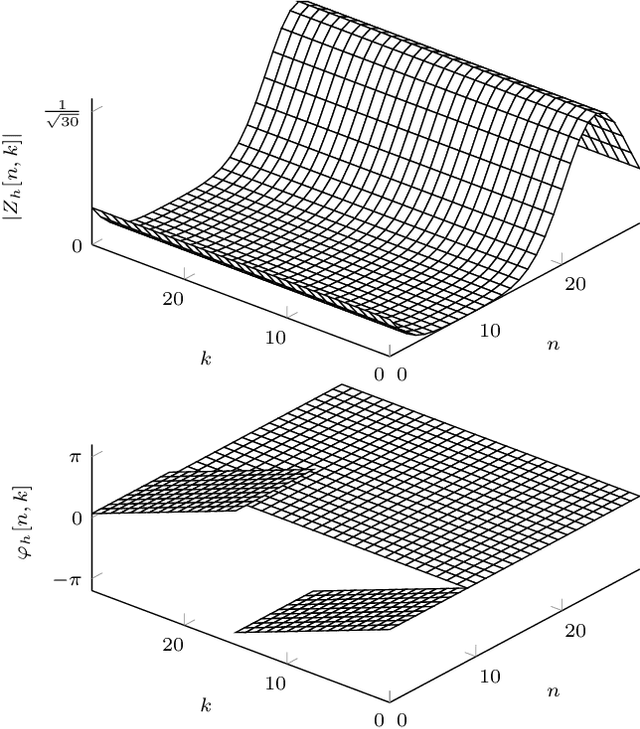
In orthogonal time frequency space (OTFS) modulation, information-carrying symbols reside in the delay-Doppler (DD) domain. By operating in the DD domain, an appealing property for communication arises: time-frequency (TF) dispersive channels encountered in high mobility environments become time-invariant. The time-invariance of the channel in the DD domain enables efficient equalizers for time-frequency dispersive channels. In this paper, we propose an OTFS system based on the discrete Zak transform. The presented formulation not only allows an efficient implementation of OTFS but also simplifies the derivation and analysis of the input-output relation of TF dispersive channel in the DD domain.
* 13 pages, 11 figures, submitted to IEEE Transaction on Wireless
Communications
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge