Optimizing Automatic Differentiation with Deep Reinforcement Learning
Paper and Code
Jun 07, 2024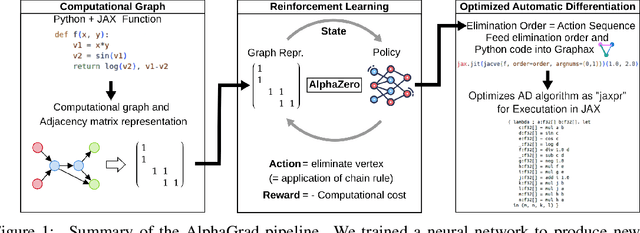
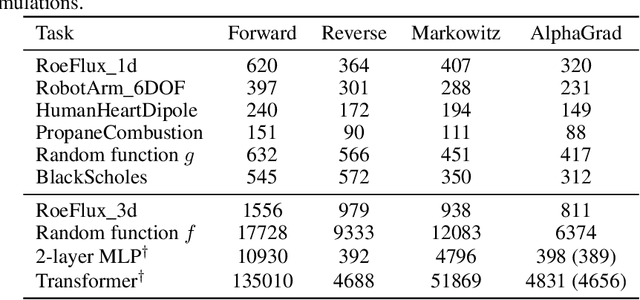
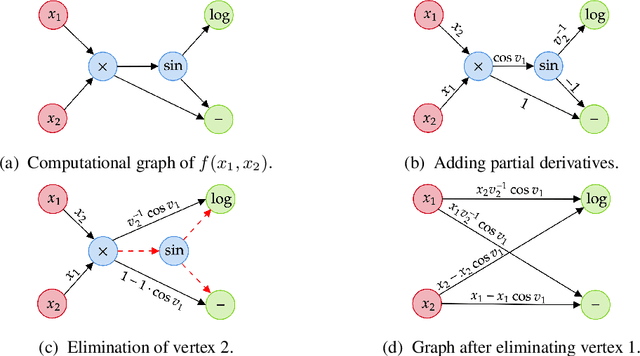
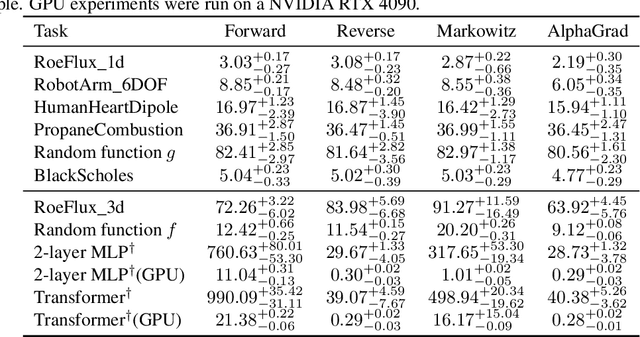
Computing Jacobians with automatic differentiation is ubiquitous in many scientific domains such as machine learning, computational fluid dynamics, robotics and finance. Even small savings in the number of computations or memory usage in Jacobian computations can already incur massive savings in energy consumption and runtime. While there exist many methods that allow for such savings, they generally trade computational efficiency for approximations of the exact Jacobian. In this paper, we present a novel method to optimize the number of necessary multiplications for Jacobian computation by leveraging deep reinforcement learning (RL) and a concept called cross-country elimination while still computing the exact Jacobian. Cross-country elimination is a framework for automatic differentiation that phrases Jacobian accumulation as ordered elimination of all vertices on the computational graph where every elimination incurs a certain computational cost. We formulate the search for the optimal elimination order that minimizes the number of necessary multiplications as a single player game which is played by an RL agent. We demonstrate that this method achieves up to 33% improvements over state-of-the-art methods on several relevant tasks taken from diverse domains. Furthermore, we show that these theoretical gains translate into actual runtime improvements by providing a cross-country elimination interpreter in JAX that can efficiently execute the obtained elimination orders.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge