Optimality of the Discrete Fourier Transform for Beamspace Massive MU-MIMO Communication
Paper and Code
Jul 14, 2021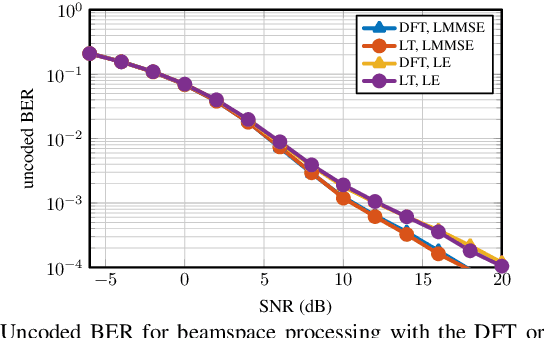
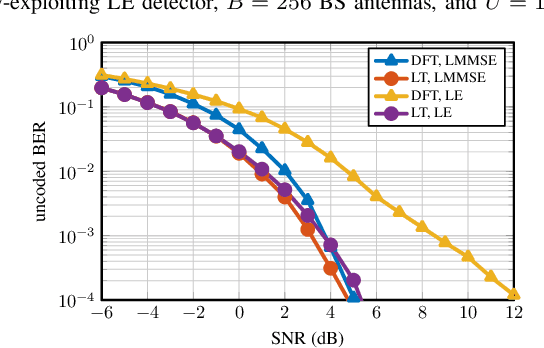
Beamspace processing is an emerging technique to reduce baseband complexity in massive multiuser (MU) multiple-input multiple-output (MIMO) communication systems operating at millimeter-wave (mmWave) and terahertz frequencies. The high directionality of wave propagation at such high frequencies ensures that only a small number of transmission paths exist between user equipments and basestation (BS). In order to resolve the sparse nature of wave propagation, beamspace processing traditionally computes a spatial discrete Fourier transform (DFT) across a uniform linear antenna array at the BS where each DFT output is associated with a specific beam. In this paper, we study optimality conditions of the DFT for sparsity-based beamspace processing with idealistic mmWave channel models and realistic channels. To this end, we propose two algorithms that learn unitary beamspace transforms using an $\ell^4$-norm-based sparsity measure, and we investigate their optimality theoretically and via simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge