Optimal Reduced-order Modeling of Bipedal Locomotion
Paper and Code
Sep 23, 2019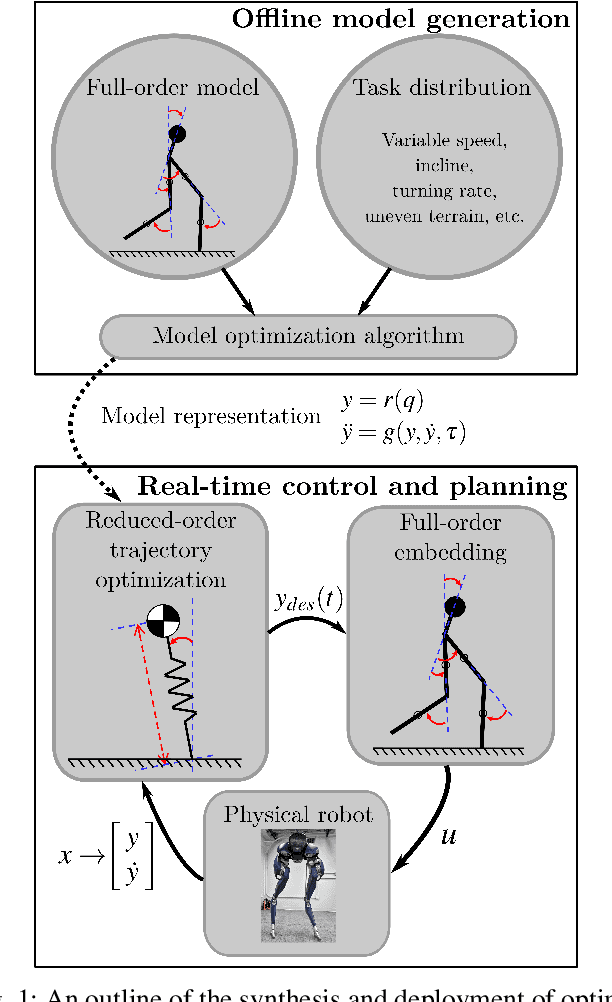
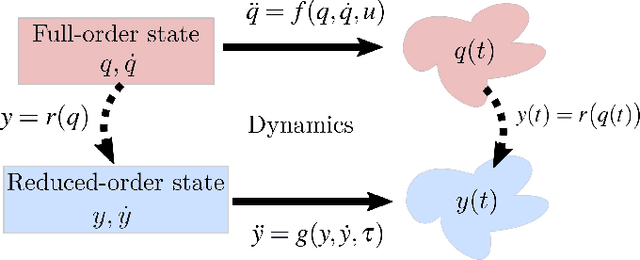
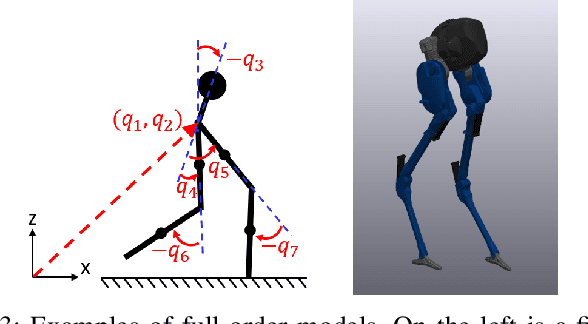
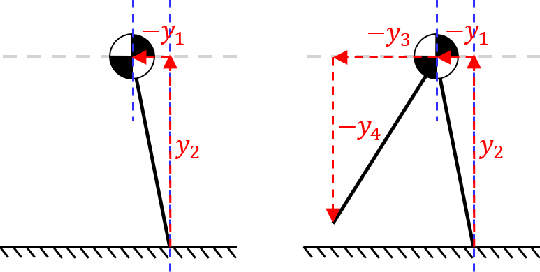
State-of-the-art approaches to legged locomotion are widely dependent on the use of models like the linear inverted pendulum (LIP) and the spring-loaded inverted pendulum (SLIP), popular because their simplicity enables a wide array of tools for planning, control, and analysis. However, they inevitably limit the ability to execute complex tasks or agile maneuvers. In this work, we aim to automatically synthesize models that remain low-dimensional but retain the capabilities of the high-dimensional system. For example, if one were to restore a small degree of complexity to LIP, SLIP, or a similar model, our approach discovers the form of that additional complexity which optimizes performance. In this paper, we define a class of reduced-order models and provide an algorithm for optimization within this class. To demonstrate our method, we optimize models for walking at a range of speeds and ground inclines, for both a five-link model and the Cassie bipedal robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge