Optimal Receive Filter Design for Misaligned Over-the-Air Computation
Paper and Code
Sep 27, 2023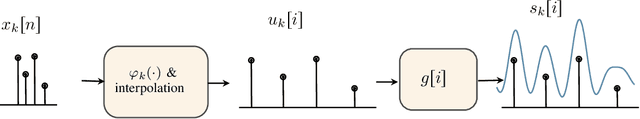
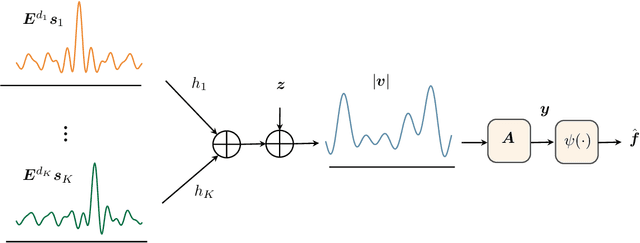
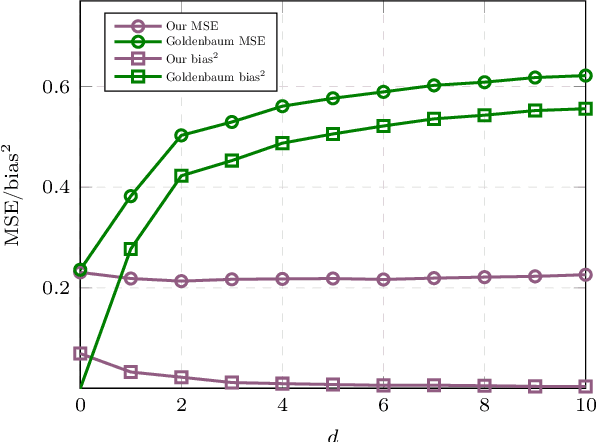
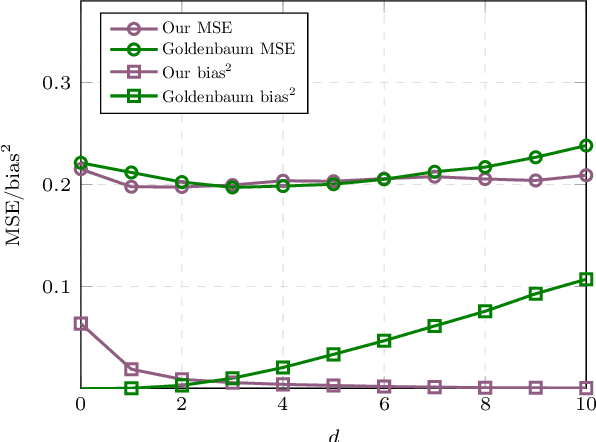
Over-the-air computation (OAC) is a promising wireless communication method for aggregating data from many devices in dense wireless networks. The fundamental idea of OAC is to exploit signal superposition to compute functions of multiple simultaneously transmitted signals. However, the time- and phase-alignment of these superimposed signals have a significant effect on the quality of function computation. In this study, we analyze the OAC problem for a system with unknown random time delays and phase shifts. We show that the classical matched filter does not produce optimal results, and generates bias in the function estimates. To counteract this, we propose a new filter design and show that, under a bound on the maximum time delay, it is possible to achieve unbiased function computation. Additionally, we propose a Tikhonov regularization problem that produces an optimal filter given a tradeoff between the bias and noise-induced variance of the function estimates. When the time delays are long compared to the length of the transmitted pulses, our filter vastly outperforms the matched filter both in terms of bias and mean-squared error (MSE). For shorter time delays, our proposal yields similar MSE as the matched filter, while reducing the bias.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge