Optimal Query Complexities for Dynamic Trace Estimation
Paper and Code
Sep 30, 2022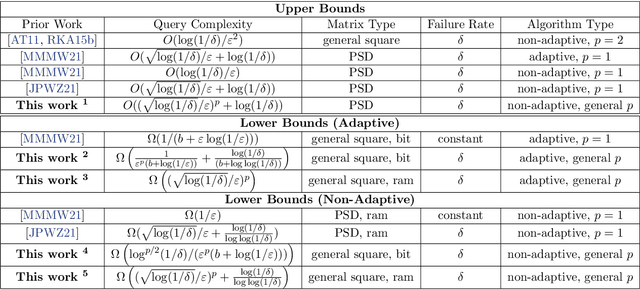
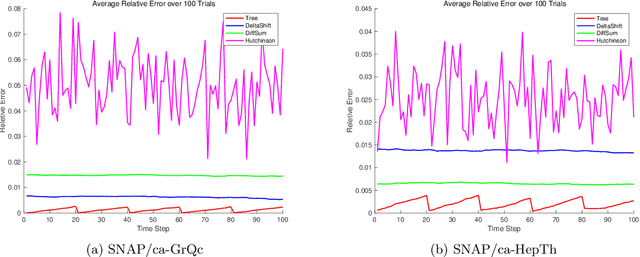
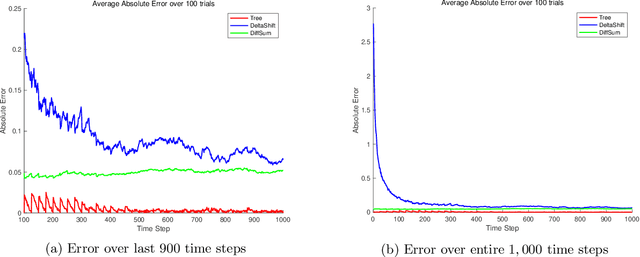
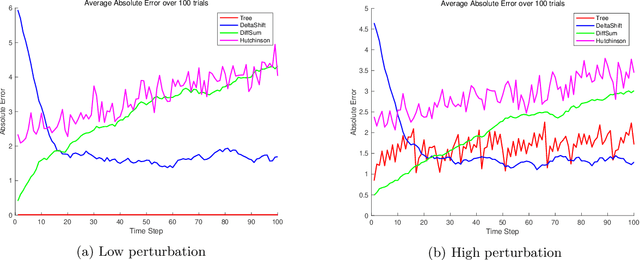
We consider the problem of minimizing the number of matrix-vector queries needed for accurate trace estimation in the dynamic setting where our underlying matrix is changing slowly, such as during an optimization process. Specifically, for any $m$ matrices $A_1,...,A_m$ with consecutive differences bounded in Schatten-$1$ norm by $\alpha$, we provide a novel binary tree summation procedure that simultaneously estimates all $m$ traces up to $\epsilon$ error with $\delta$ failure probability with an optimal query complexity of $\widetilde{O}\left(m \alpha\sqrt{\log(1/\delta)}/\epsilon + m\log(1/\delta)\right)$, improving the dependence on both $\alpha$ and $\delta$ from Dharangutte and Musco (NeurIPS, 2021). Our procedure works without additional norm bounds on $A_i$ and can be generalized to a bound for the $p$-th Schatten norm for $p \in [1,2]$, giving a complexity of $\widetilde{O}\left(m \alpha\left(\sqrt{\log(1/\delta)}/\epsilon\right)^p +m \log(1/\delta)\right)$. By using novel reductions to communication complexity and information-theoretic analyses of Gaussian matrices, we provide matching lower bounds for static and dynamic trace estimation in all relevant parameters, including the failure probability. Our lower bounds (1) give the first tight bounds for Hutchinson's estimator in the matrix-vector product model with Frobenius norm error even in the static setting, and (2) are the first unconditional lower bounds for dynamic trace estimation, resolving open questions of prior work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge