Optimal Neural Network Approximation of Wasserstein Gradient Direction via Convex Optimization
Paper and Code
May 26, 2022
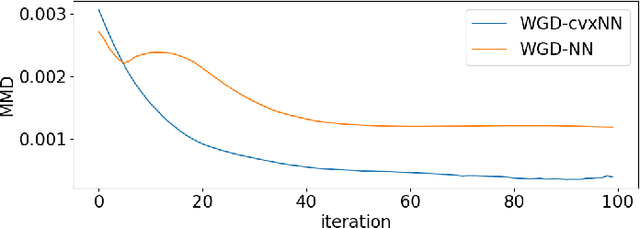
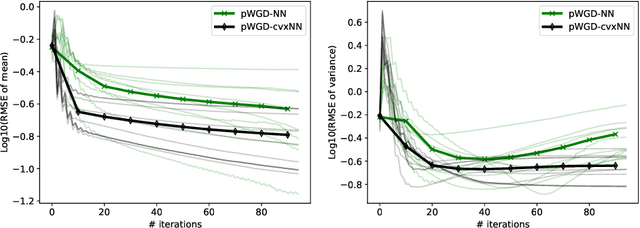

The computation of Wasserstein gradient direction is essential for posterior sampling problems and scientific computing. The approximation of the Wasserstein gradient with finite samples requires solving a variational problem. We study the variational problem in the family of two-layer networks with squared-ReLU activations, towards which we derive a semi-definite programming (SDP) relaxation. This SDP can be viewed as an approximation of the Wasserstein gradient in a broader function family including two-layer networks. By solving the convex SDP, we obtain the optimal approximation of the Wasserstein gradient direction in this class of functions. Numerical experiments including PDE-constrained Bayesian inference and parameter estimation in COVID-19 modeling demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge