Optimal Filter Selection for Multispectral Object Classification Using Fast Binary Search
Paper and Code
Sep 16, 2022
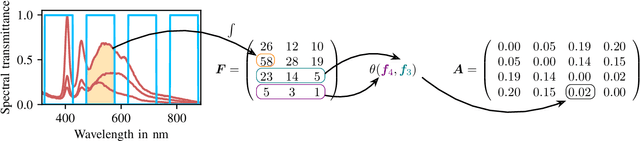


When designing multispectral imaging systems for classifying different spectra it is necessary to choose a small number of filters from a set with several hundred different ones. Tackling this problem by full search leads to a tremendous number of possibilities to check and is NP-hard. In this paper we introduce a novel fast binary search for optimal filter selection that guarantees a minimum distance metric between the different spectra to classify. In our experiments, this procedure reaches the same optimal solution as with full search at much lower complexity. The desired number of filters influences the full search in factorial order while the fast binary search stays constant. Thus, fast binary search allows to find the optimal solution of all combinations in an adequate amount of time and avoids prevailing heuristics. Moreover, our fast binary search algorithm outperforms other filter selection techniques in terms of misclassified spectra in a real-world classification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge