Optimal Beamforming of RIS-Aided Wireless Communications: An Alternating Inner Product Maximization Approach
Paper and Code
May 10, 2024
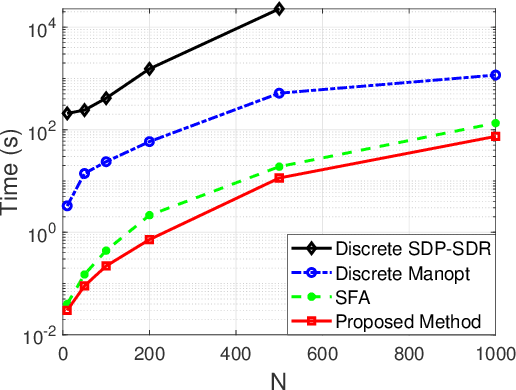


This paper investigates a general discrete $\ell_p$-norm maximization problem, with the power enhancement at steering directions through reconfigurable intelligent surfaces (RISs) as an instance. We propose a mathematically concise iterative framework composed of alternating inner product maximizations, well-suited for addressing $\ell_1$- and $\ell_2$-norm maximizations with either discrete or continuous uni-modular variable constraints. The iteration is proven to be monotonically non-decreasing. Moreover, this framework exhibits a distinctive capability to mitigate performance degradation due to discrete quantization, establishing it as the first post-rounding lifting approach applicable to any algorithm intended for the continuous solution. Additionally, as an integral component of the alternating iterations framework, we present a divide-and-sort (DaS) method to tackle the discrete inner product maximization problem. In the realm of $\ell_\infty$-norm maximization with discrete uni-modular constraints, the DaS ensures the identification of the global optimum with polynomial search complexity. We validate the effectiveness of the alternating inner product maximization framework in beamforming through RISs using both numerical experiments and field trials on prototypes. The results demonstrate that the proposed approach achieves higher power enhancement and outperforms other competitors. Finally, we show that discrete phase configurations with moderate quantization bits (e.g., 4-bit) exhibit comparable performance to continuous configurations in terms of power gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge