Optimal 1-NN Prototypes for Pathological Geometries
Paper and Code
Oct 31, 2020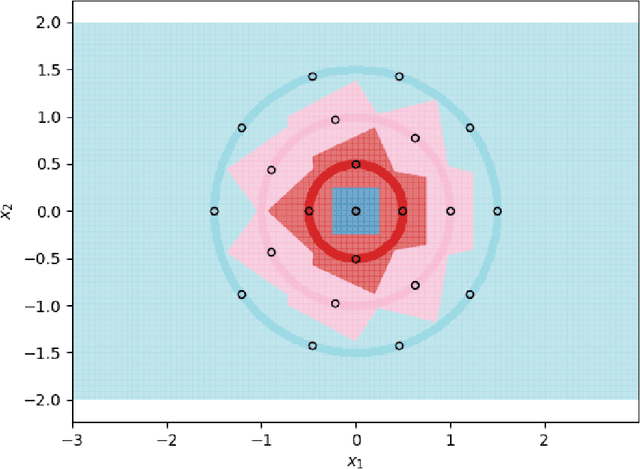
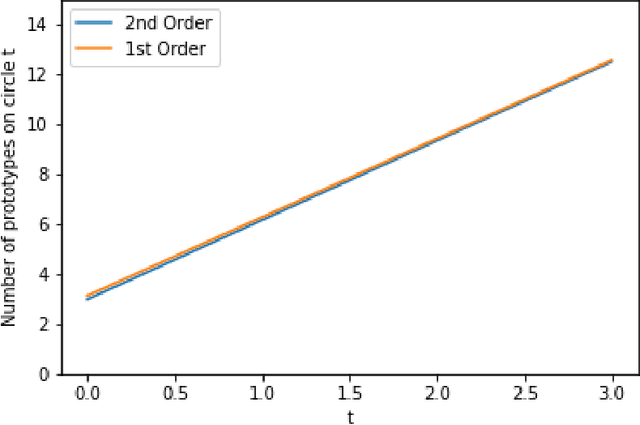
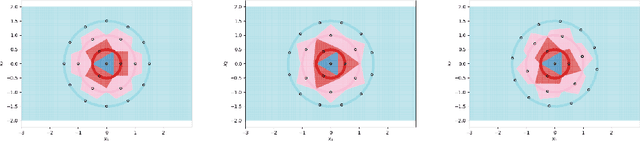
Using prototype methods to reduce the size of training datasets can drastically reduce the computational cost of classification with instance-based learning algorithms like the k-Nearest Neighbour classifier. The number and distribution of prototypes required for the classifier to match its original performance is intimately related to the geometry of the training data. As a result, it is often difficult to find the optimal prototypes for a given dataset, and heuristic algorithms are used instead. However, we consider a particularly challenging setting where commonly used heuristic algorithms fail to find suitable prototypes and show that the optimal prototypes can instead be found analytically. We also propose an algorithm for finding nearly-optimal prototypes in this setting, and use it to empirically validate the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge