Online Planning in Uncertain and Dynamic Environment in the Presence of Multiple Mobile Vehicles
Paper and Code
Sep 08, 2020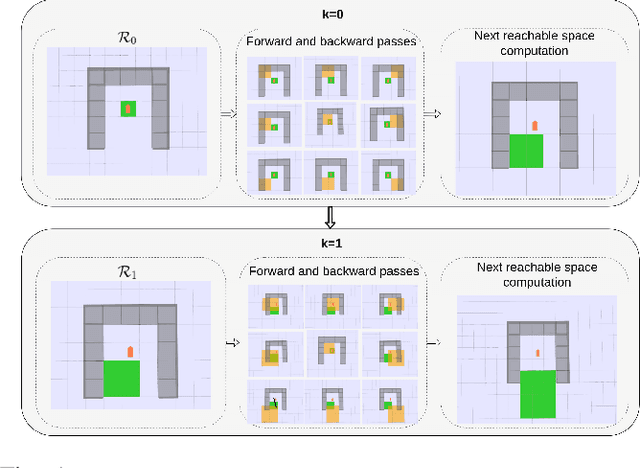

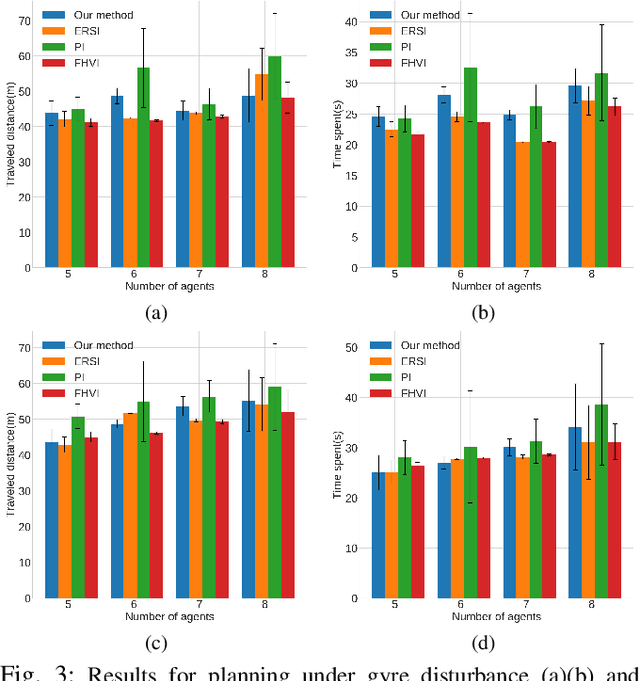

We investigate the autonomous navigation of a mobile robot in the presence of other moving vehicles under time-varying uncertain environmental disturbances. We first predict the future state distributions of other vehicles to account for their uncertain behaviors affected by the time-varying disturbances. We then construct a dynamic-obstacle-aware reachable space that contains states with high probabilities to be reached by the robot, within which the optimal policy is searched. Since, in general, the dynamics of both the vehicle and the environmental disturbances are nonlinear, we utilize a nonlinear Gaussian filter -- the unscented transform -- to approximate the future state distributions. Finally, the forward reachable space computation and backward policy search are iterated until convergence. Extensive simulation evaluations have revealed significant advantages of this proposed method in terms of computation time, decision accuracy, and planning reliability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge