Online Multiclass Boosting
Paper and Code
Feb 25, 2018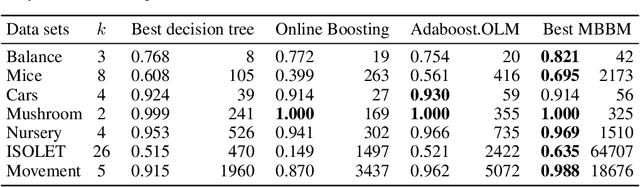
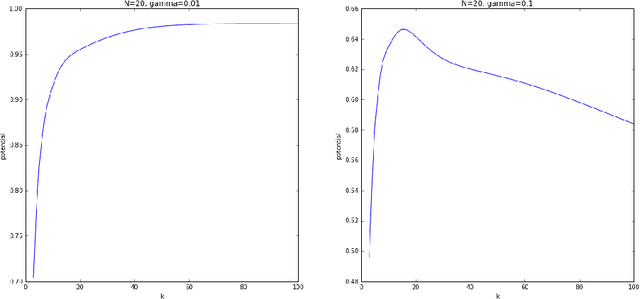
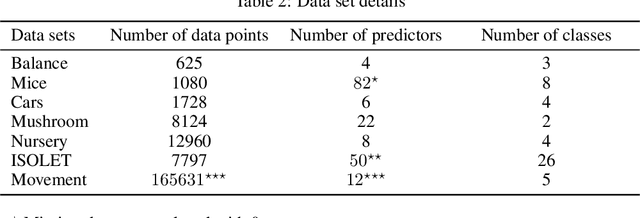
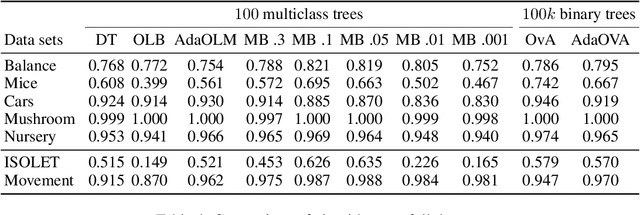
Recent work has extended the theoretical analysis of boosting algorithms to multiclass problems and to online settings. However, the multiclass extension is in the batch setting and the online extensions only consider binary classification. We fill this gap in the literature by defining, and justifying, a weak learning condition for online multiclass boosting. This condition leads to an optimal boosting algorithm that requires the minimal number of weak learners to achieve a certain accuracy. Additionally, we propose an adaptive algorithm which is near optimal and enjoys an excellent performance on real data due to its adaptive property.
* 28 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge