Online Limited Memory Neural-Linear Bandits with Likelihood Matching

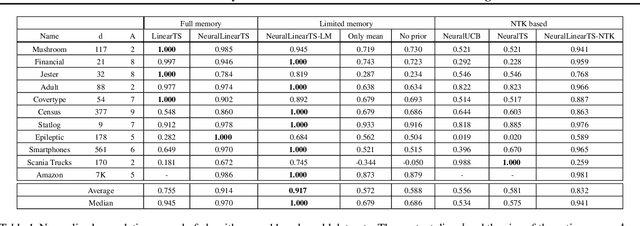
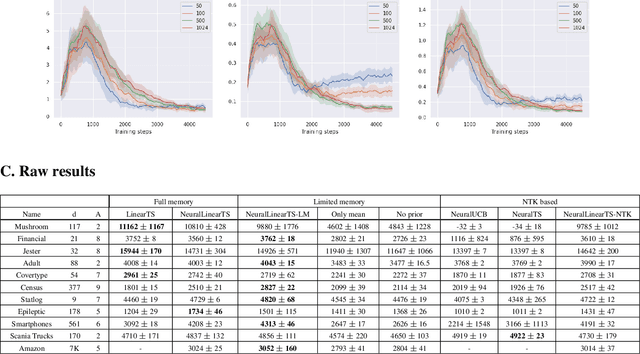
We study neural-linear bandits for solving problems where both exploration and representation learning play an important role. Neural-linear bandits leverage the representation power of Deep Neural Networks (DNNs) and combine it with efficient exploration mechanisms designed for linear contextual bandits on top of the last hidden layer. A recent analysis of DNNs in the "infinite-width" regime suggests that when these models are trained with gradient descent the optimal solution is close to the initialization point and the DNN can be viewed as a kernel machine. As a result, it is possible to exploit linear exploration algorithms on top of a DNN via the kernel construction. The problem is that in practice the kernel changes during the learning process and the agent's performance degrades. This can be resolved by recomputing new uncertainty estimations with stored data. Nevertheless, when the buffer's size is limited, a phenomenon called catastrophic forgetting emerges. Instead, we propose a likelihood matching algorithm that is resilient to catastrophic forgetting and is completely online. We perform simulations on a variety of datasets and observe that our algorithm achieves comparable performance to the unlimited memory approach while exhibits resilience to catastrophic forgetting.