Online Learning to Sample
Paper and Code
Mar 15, 2016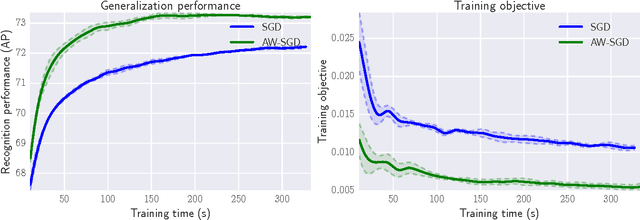

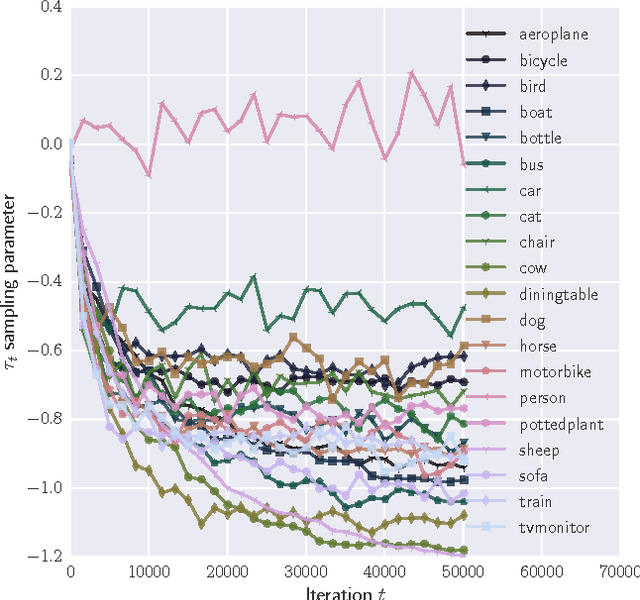
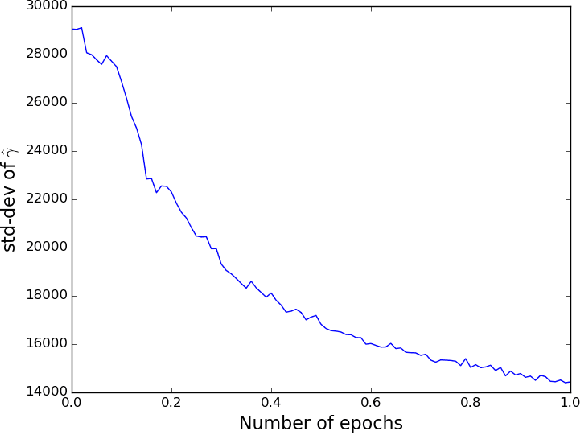
Stochastic Gradient Descent (SGD) is one of the most widely used techniques for online optimization in machine learning. In this work, we accelerate SGD by adaptively learning how to sample the most useful training examples at each time step. First, we show that SGD can be used to learn the best possible sampling distribution of an importance sampling estimator. Second, we show that the sampling distribution of an SGD algorithm can be estimated online by incrementally minimizing the variance of the gradient. The resulting algorithm - called Adaptive Weighted SGD (AW-SGD) - maintains a set of parameters to optimize, as well as a set of parameters to sample learning examples. We show that AWSGD yields faster convergence in three different applications: (i) image classification with deep features, where the sampling of images depends on their labels, (ii) matrix factorization, where rows and columns are not sampled uniformly, and (iii) reinforcement learning, where the optimized and exploration policies are estimated at the same time, where our approach corresponds to an off-policy gradient algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge