Online Joint State Inference and Learning of Partially Unknown State-Space Models

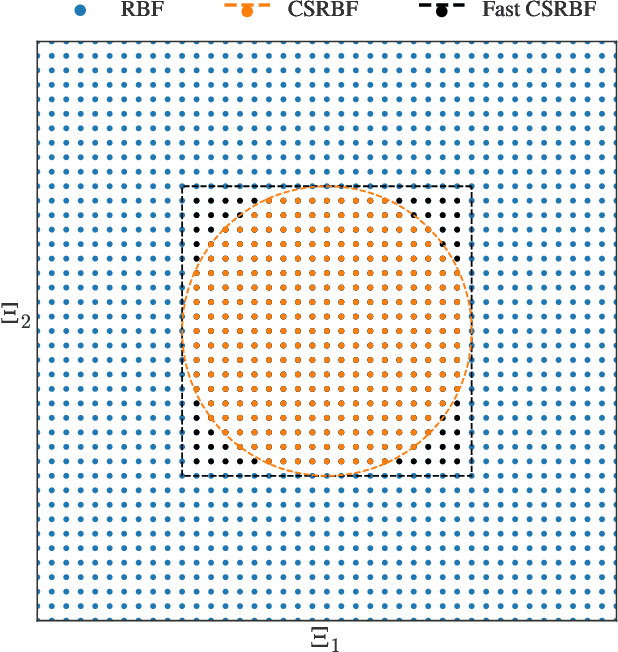
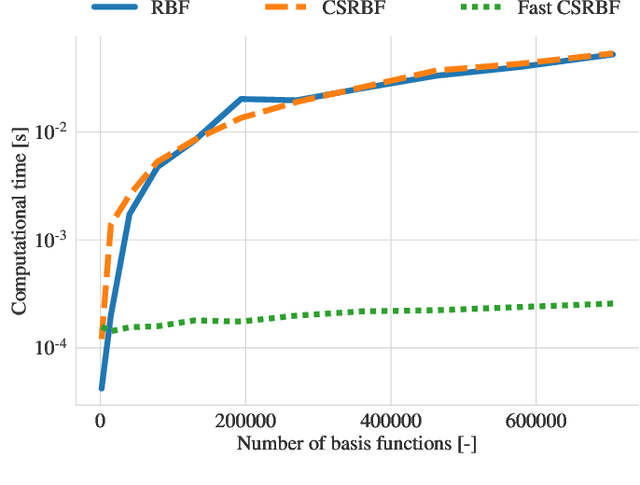
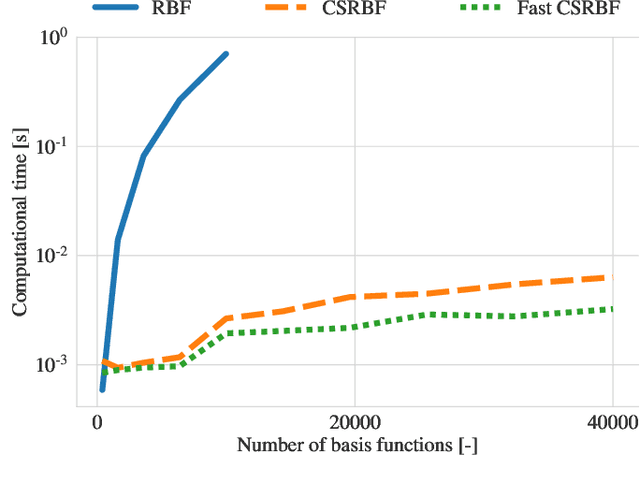
A computationally efficient method for online joint state inference and dynamical model learning is presented. The dynamical model combines an a priori known state-space model with a radial basis function expansion representing unknown system dynamics. Thus, the model is inherently adaptive and can learn unknown and changing system dynamics on-the-fly. Still, by including prior knowledge in the model description, a minimum of estimation performance can be guaranteed already from the start, which is of utmost importance in, e.g., safety-critical applications. The method uses an extended Kalman filter approach to jointly estimate the state of the system and learn the system properties, via the parameters of the basis function expansion. By using compact radial basis functions and an approximate Kalman gain, the computational complexity is considerably reduced compared to similar approaches. The approximation works well when the system dynamics exhibit limited correlation between points well separated in the state-space domain. The method is exemplified via two intelligent vehicle applications where it is shown to: (i) have essentially identical system dynamics estimation performance compared to similar non-real-time algorithms, and (ii) be real-time applicable to large-scale problems.