One Sample Fits All: Approximating All Probabilistic Values Simultaneously and Efficiently
Paper and Code
Oct 31, 2024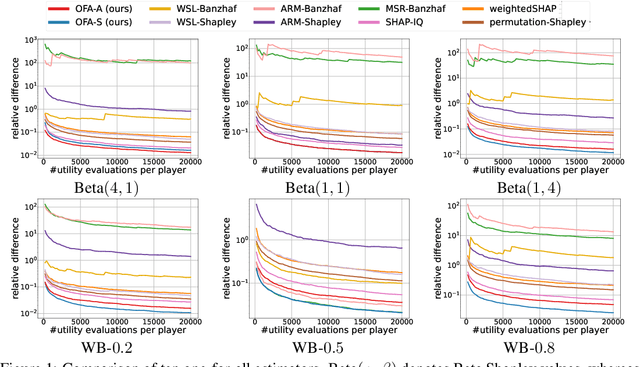

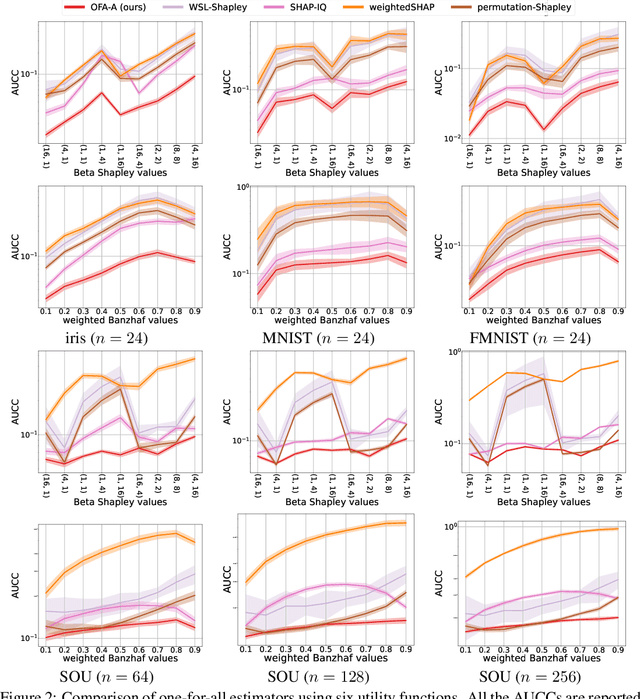
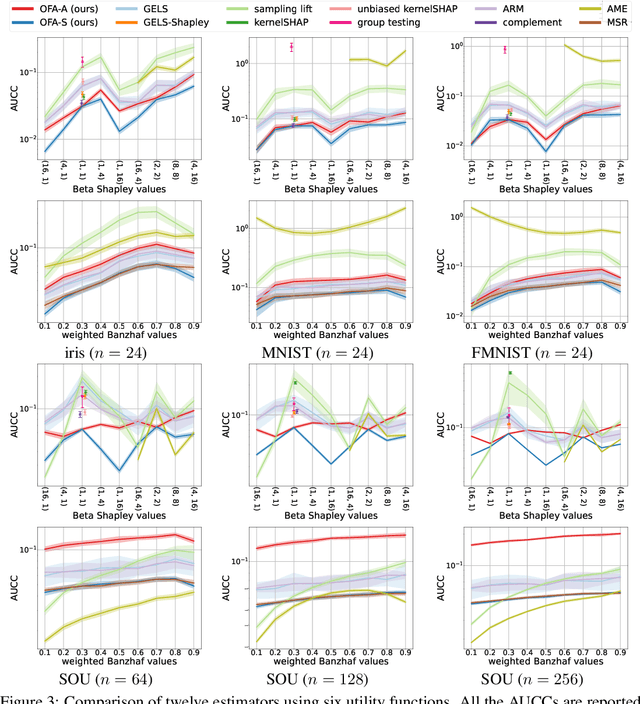
The concept of probabilistic values, such as Beta Shapley values and weighted Banzhaf values, has gained recent attention in applications like feature attribution and data valuation. However, exact computation of these values is often exponentially expensive, necessitating approximation techniques. Prior research has shown that the choice of probabilistic values significantly impacts downstream performance, with no universally superior option. Consequently, one may have to approximate multiple candidates and select the best-performing one. Although there have been many efforts to develop efficient estimators, none are intended to approximate all probabilistic values both simultaneously and efficiently. In this work, we embark on the first exploration of achieving this goal. Adhering to the principle of maximum sample reuse, we propose a one-sample-fits-all framework parameterized by a sampling vector to approximate intermediate terms that can be converted to any probabilistic value without amplifying scalars. Leveraging the concept of $ (\epsilon, \delta) $-approximation, we theoretically identify a key formula that effectively determines the convergence rate of our framework. By optimizing the sampling vector using this formula, we obtain i) a one-for-all estimator that achieves the currently best time complexity for all probabilistic values on average, and ii) a faster generic estimator with the sampling vector optimally tuned for each probabilistic value. Particularly, our one-for-all estimator achieves the fastest convergence rate on Beta Shapley values, including the well-known Shapley value, both theoretically and empirically. Finally, we establish a connection between probabilistic values and the least square regression used in (regularized) datamodels, showing that our one-for-all estimator can solve a family of datamodels simultaneously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge