On time series clustering with k-means
Paper and Code
Oct 18, 2024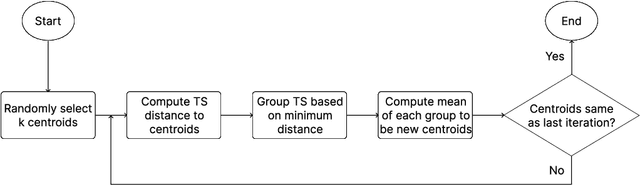

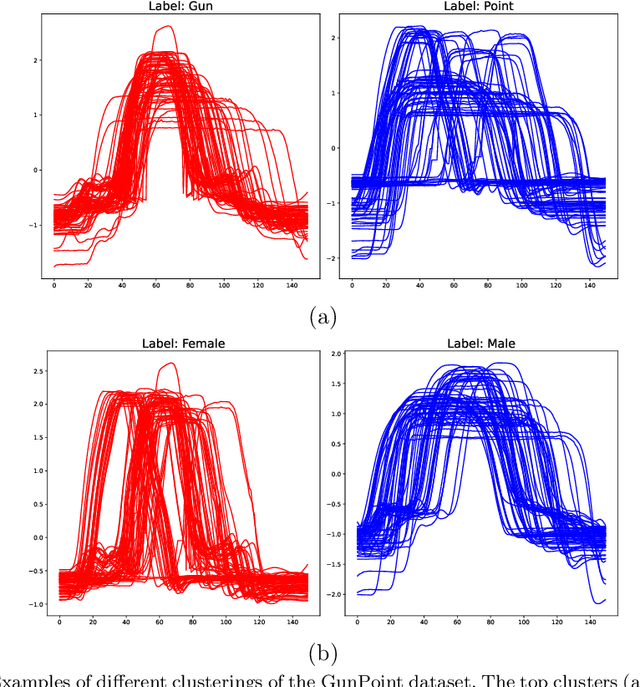

There is a long history of research into time series clustering using distance-based partitional clustering. Many of the most popular algorithms adapt k-means (also known as Lloyd's algorithm) to exploit time dependencies in the data by specifying a time series distance function. However, these algorithms are often presented with k-means configured in various ways, altering key parameters such as the initialisation strategy. This variability makes it difficult to compare studies because k-means is known to be highly sensitive to its configuration. To address this, we propose a standard Lloyd's-based model for TSCL that adopts an end-to-end approach, incorporating a specialised distance function not only in the assignment step but also in the initialisation and stopping criteria. By doing so, we create a unified structure for comparing seven popular Lloyd's-based TSCL algorithms. This common framework enables us to more easily attribute differences in clustering performance to the distance function itself, rather than variations in the k-means configuration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge