On the use of Harrell's C for clinical risk prediction via random survival forests

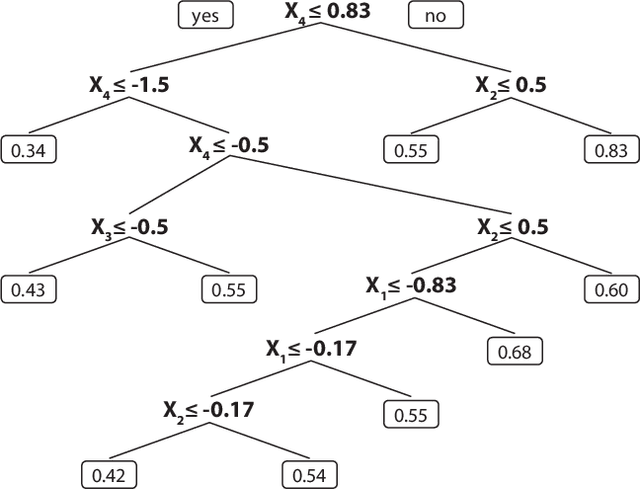
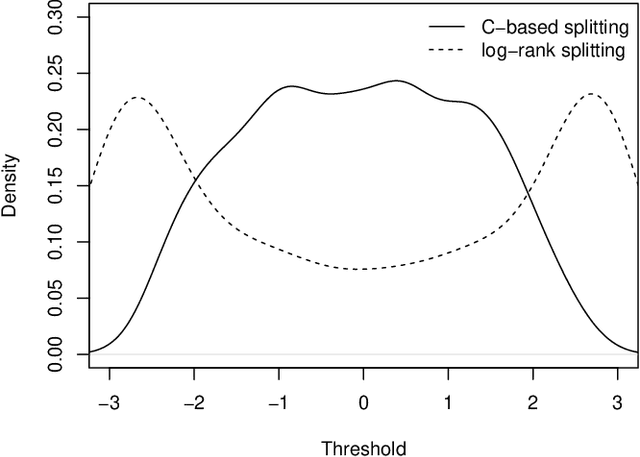
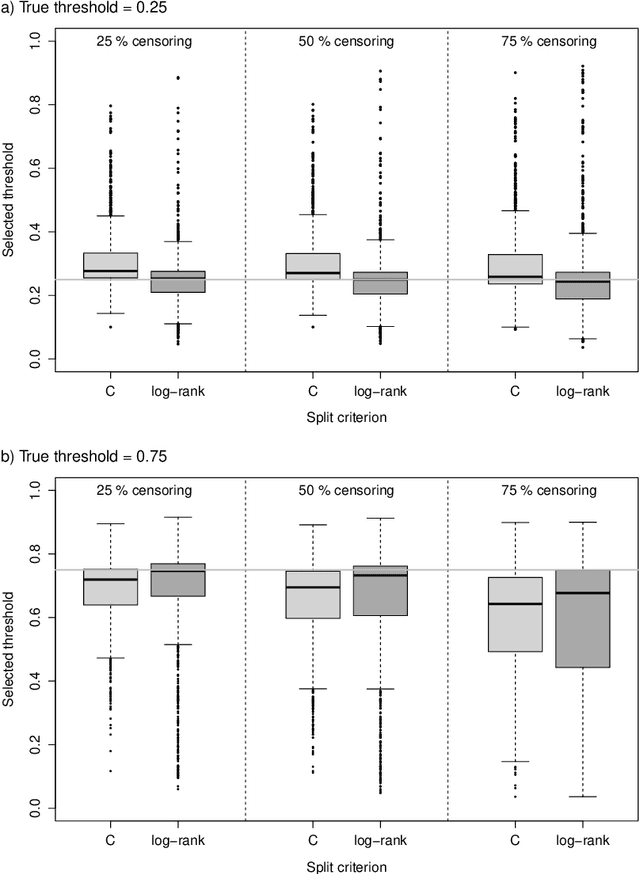
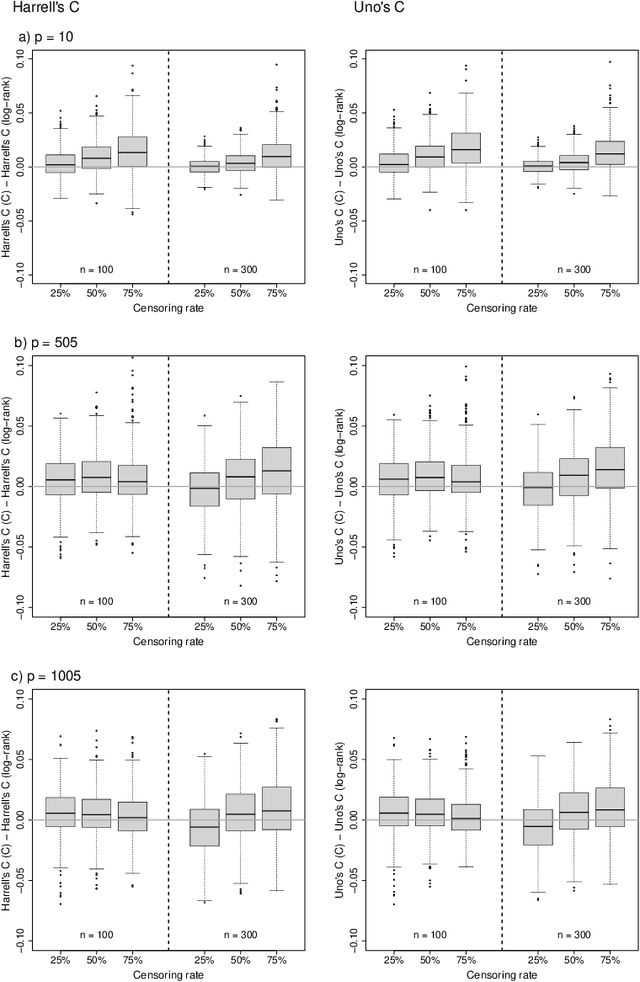
Random survival forests (RSF) are a powerful method for risk prediction of right-censored outcomes in biomedical research. RSF use the log-rank split criterion to form an ensemble of survival trees. The most common approach to evaluate the prediction accuracy of a RSF model is Harrell's concordance index for survival data ('C index'). Conceptually, this strategy implies that the split criterion in RSF is different from the evaluation criterion of interest. This discrepancy can be overcome by using Harrell's C for both node splitting and evaluation. We compare the difference between the two split criteria analytically and in simulation studies with respect to the preference of more unbalanced splits, termed end-cut preference (ECP). Specifically, we show that the log-rank statistic has a stronger ECP compared to the C index. In simulation studies and with the help of two medical data sets we demonstrate that the accuracy of RSF predictions, as measured by Harrell's C, can be improved if the log-rank statistic is replaced by the C index for node splitting. This is especially true in situations where the censoring rate or the fraction of informative continuous predictor variables is high. Conversely, log-rank splitting is preferable in noisy scenarios. Both C-based and log-rank splitting are implemented in the R~package ranger. We recommend Harrell's C as split criterion for use in smaller scale clinical studies and the log-rank split criterion for use in large-scale 'omics' studies.