On the stability analysis of optimal state feedbacks as represented by deep neural models
Paper and Code
Dec 07, 2018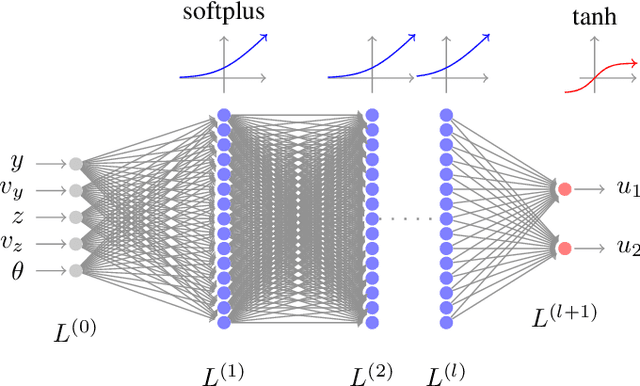
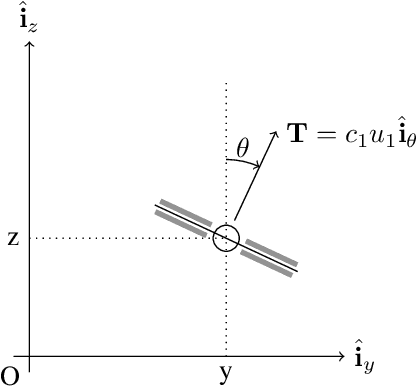
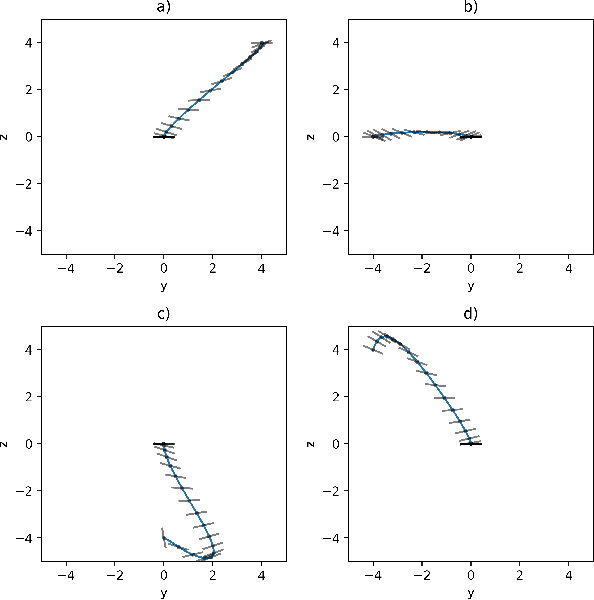
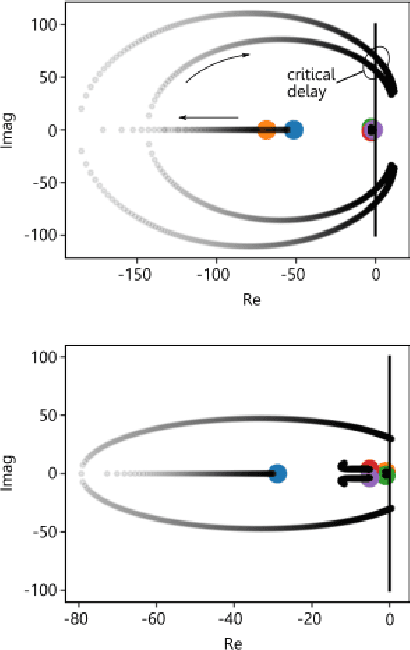
Research has shown how the optimal feedback control of several non linear systems of interest in aerospace applications can be represented by deep neural architectures and trained using techniques including imitation learning, reinforcement learning and evolutionary algorithms. Such deep architectures are here also referred to as Guidance and Control Networks, or G&CNETs. It is difficult to provide theoretical proofs on the control stability of such neural control architectures in general, and G&CNETs in particular, to perturbations, time delays or model uncertainties or to compute stability margins and trace them back to the network training process or to its architecture. In most cases the analysis of the trained network is performed via Monte Carlo experiments and practitioners renounce to any formal guarantee. This lack of validation naturally leads to scepticism especially in cases where safety and validation are of paramount importance such as is the case, for example, in the automotive or space industry. In an attempt to narrow the gap between deep learning research and control theory, we propose a new methodology based on differential algebra and automated differentiation to obtain formal guarantees on the behaviour of neural based control systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge