On the optimization and generalization of overparameterized implicit neural networks
Paper and Code
Sep 30, 2022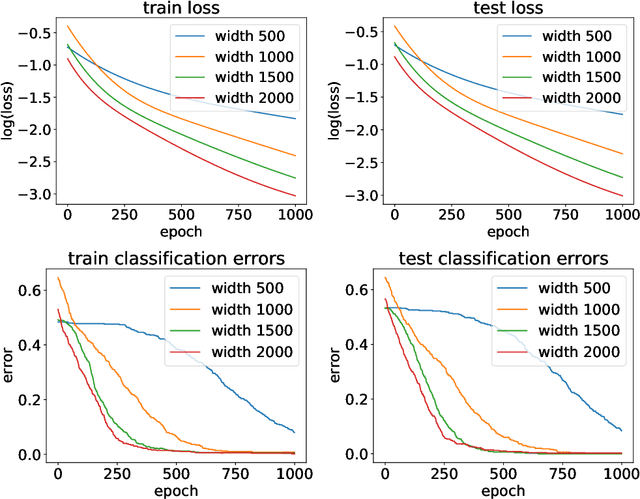
Implicit neural networks have become increasingly attractive in the machine learning community since they can achieve competitive performance but use much less computational resources. Recently, a line of theoretical works established the global convergences for first-order methods such as gradient descent if the implicit networks are over-parameterized. However, as they train all layers together, their analyses are equivalent to only studying the evolution of the output layer. It is unclear how the implicit layer contributes to the training. Thus, in this paper, we restrict ourselves to only training the implicit layer. We show that global convergence is guaranteed, even if only the implicit layer is trained. On the other hand, the theoretical understanding of when and how the training performance of an implicit neural network can be generalized to unseen data is still under-explored. Although this problem has been studied in standard feed-forward networks, the case of implicit neural networks is still intriguing since implicit networks theoretically have infinitely many layers. Therefore, this paper investigates the generalization error for implicit neural networks. Specifically, we study the generalization of an implicit network activated by the ReLU function over random initialization. We provide a generalization bound that is initialization sensitive. As a result, we show that gradient flow with proper random initialization can train a sufficient over-parameterized implicit network to achieve arbitrarily small generalization errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge