On the Low-Complexity of Fair Learning for Combinatorial Multi-Armed Bandit

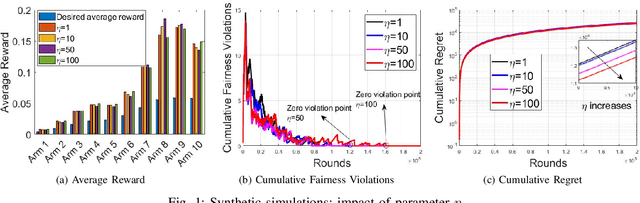
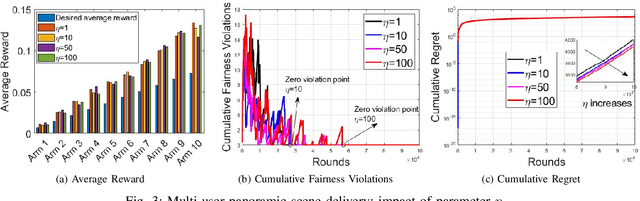
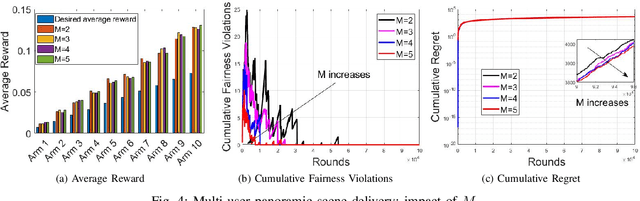
Combinatorial Multi-Armed Bandit with fairness constraints is a framework where multiple arms form a super arm and can be pulled in each round under uncertainty to maximize cumulative rewards while ensuring the minimum average reward required by each arm. The existing pessimistic-optimistic algorithm linearly combines virtual queue-lengths (tracking the fairness violations) and Upper Confidence Bound estimates as a weight for each arm and selects a super arm with the maximum total weight. The number of super arms could be exponential to the number of arms in many scenarios. In wireless networks, interference constraints can cause the number of super arms to grow exponentially with the number of arms. Evaluating all the feasible super arms to find the one with the maximum total weight can incur extremely high computational complexity in the pessimistic-optimistic algorithm. To avoid this, we develop a low-complexity fair learning algorithm based on the so-called pick-and-compare approach that involves randomly picking $M$ feasible super arms to evaluate. By setting $M$ to a constant, the number of comparison steps in the pessimistic-optimistic algorithm can be reduced to a constant, thereby significantly reducing the computational complexity. Our theoretical proof shows this low-complexity design incurs only a slight sacrifice in fairness and regret performance. Finally, we validate the theoretical result by extensive simulations.