On the Learning Dynamics of Two-layer Nonlinear Convolutional Neural Networks
Paper and Code
May 24, 2019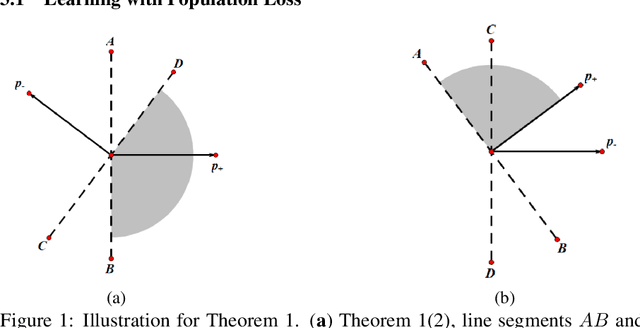
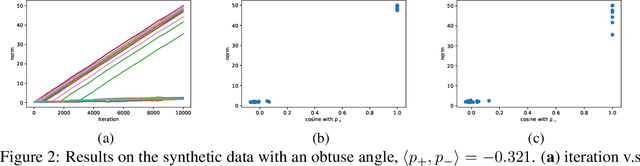
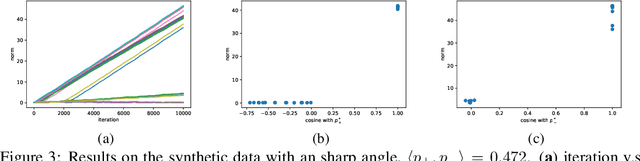

Convolutional neural networks (CNNs) have achieved remarkable performance in various fields, particularly in the domain of computer vision. However, why this architecture works well remains to be a mystery. In this work we move a small step toward understanding the success of CNNs by investigating the learning dynamics of a two-layer nonlinear convolutional neural network over some specific data distributions. Rather than the typical Gaussian assumption for input data distribution, we consider a more realistic setting that each data point (e.g. image) contains a specific pattern determining its class label. Within this setting, we both theoretically and empirically show that some convolutional filters will learn the key patterns in data and the norm of these filters will dominate during the training process with stochastic gradient descent. And with any high probability, when the number of iterations is sufficiently large, the CNN model could obtain 100% accuracy over the considered data distributions. Our experiments demonstrate that for practical image classification tasks our findings still hold to some extent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge