On the Geometry of Deep Learning
Paper and Code
Aug 09, 2024
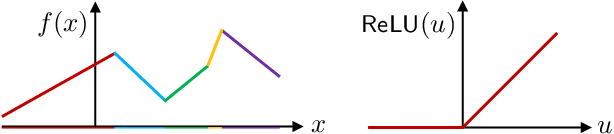


In this paper, we overview one promising avenue of progress at the mathematical foundation of deep learning: the connection between deep networks and function approximation by affine splines (continuous piecewise linear functions in multiple dimensions). In particular, we will overview work over the past decade on understanding certain geometrical properties of a deep network's affine spline mapping, in particular how it tessellates its input space. As we will see, the affine spline connection and geometrical viewpoint provide a powerful portal through which to view, analyze, and improve the inner workings of a deep network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge