On the Equivalence between Node Embeddings and Structural Graph Representations

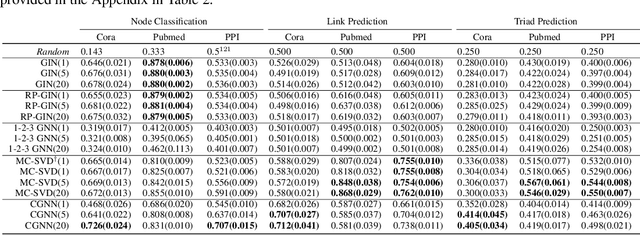
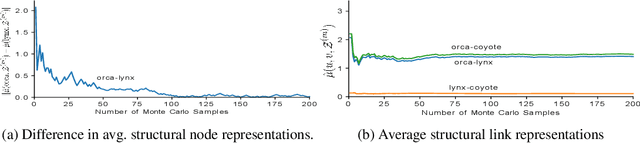
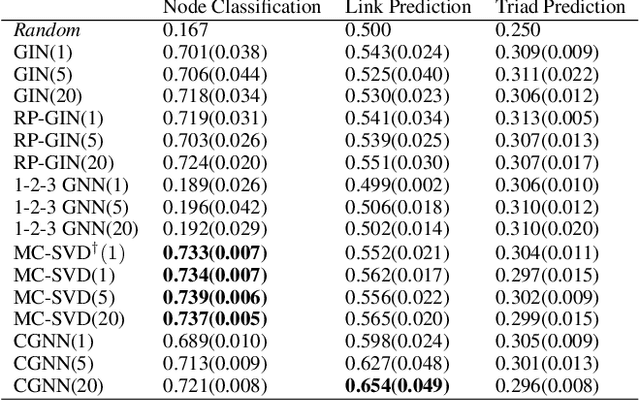
This work provides the first unifying theoretical framework for node embeddings and structural graph representations, bridging methods like matrix factorization and graph neural networks. Using invariant theory, we show that the relationship between structural representations and node embeddings is analogous to that of a distribution and its samples. We prove that all tasks that can be performed by node embeddings can also be performed by structural representations and vice-versa. We also show that the concept of transductive and inductive learning is unrelated to node embeddings and graph representations, clearing another source of confusion in the literature. Finally, we introduce new practical guidelines to generating and using node embeddings, which fixes significant shortcomings of standard operating procedures used today.