On the convergence properties of a $K$-step averaging stochastic gradient descent algorithm for nonconvex optimization
Paper and Code
May 16, 2018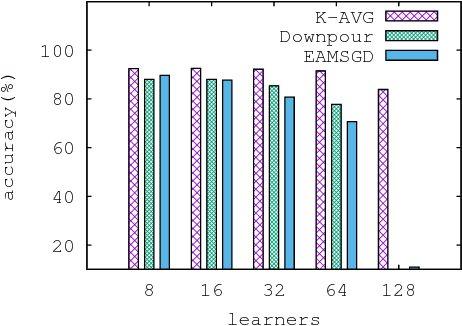
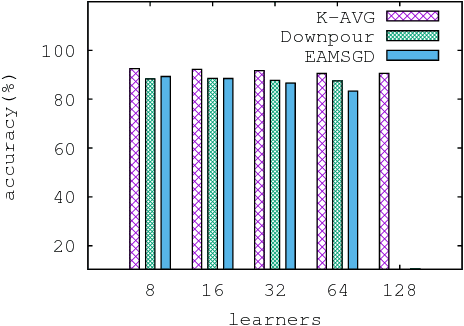
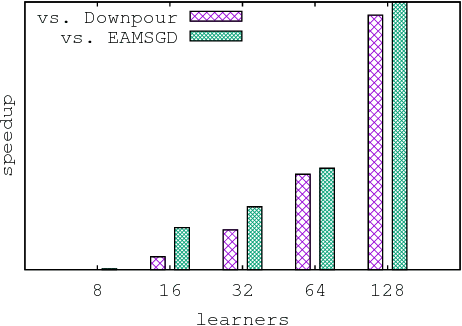
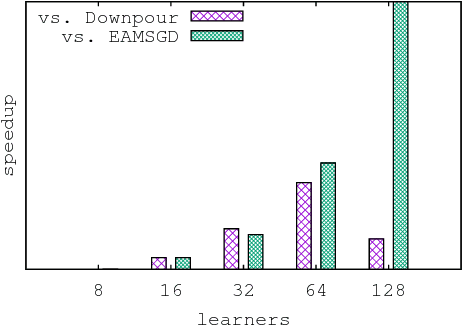
Despite their popularity, the practical performance of asynchronous stochastic gradient descent methods (ASGD) for solving large scale machine learning problems are not as good as theoretical results indicate. We adopt and analyze a synchronous K-step averaging stochastic gradient descent algorithm which we call K-AVG. We establish the convergence results of K-AVG for nonconvex objectives and explain why the K-step delay is necessary and leads to better performance than traditional parallel stochastic gradient descent which is a special case of K-AVG with $K=1$. We also show that K-AVG scales better than ASGD. Another advantage of K-AVG over ASGD is that it allows larger stepsizes. On a cluster of $128$ GPUs, K-AVG is faster than ASGD implementations and achieves better accuracies and faster convergence for \cifar dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge