On the Convergence of SARAH and Beyond

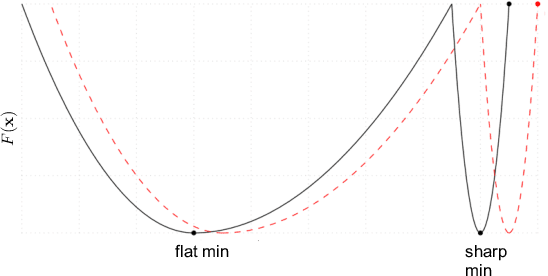
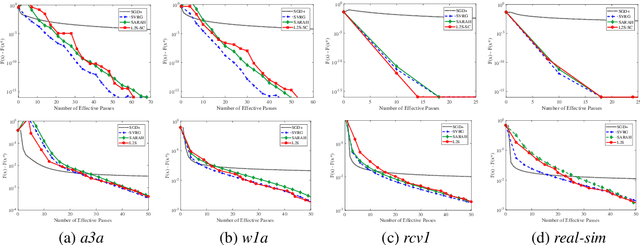
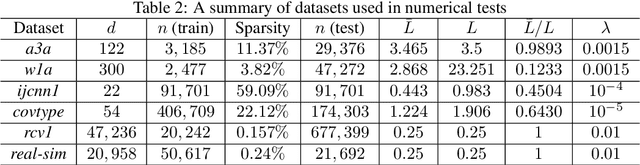
The main theme of this work is a unifying algorithm, abbreviated as L2S, that can deal with (strongly) convex and nonconvex empirical risk minimization (ERM) problems. It broadens a recently developed variance reduction method known as SARAH. L2S enjoys a linear convergence rate for strongly convex problems, which also implies the last iteration of SARAH's inner loop converges linearly. For convex problems, different from SARAH, L2S can afford step and mini-batch sizes not dependent on the data size $n$, and the complexity needed to guarantee $\mathbb{E}[\|\nabla F(\mathbf{x}) \|^2] \leq \epsilon$ is ${\cal O}(n+ n/\epsilon)$. For nonconvex problems on the other hand, the complexity is ${\cal O}(n+ \sqrt{n}/\epsilon)$. Parallel to L2S there are a few side results. Leveraging an aggressive step size, D2S is proposed, which provides a more efficient alternative to L2S and SARAH-like algorithms. Specifically, D2S requires a reduced IFO complexity of ${\cal O}\big( (n+ \bar{\kappa}) \ln (1/\epsilon) \big)$ for strongly convex problems. Moreover, to avoid the tedious selection of the optimal step size, an automatic tuning scheme is developed, which obtains comparable empirical performance with SARAH using judiciously tuned step size.