On The Convergence of Gradient Descent for Finding the Riemannian Center of Mass

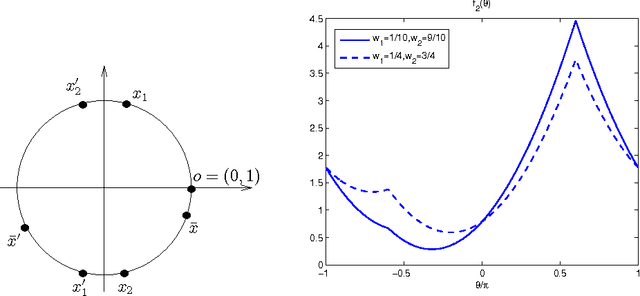
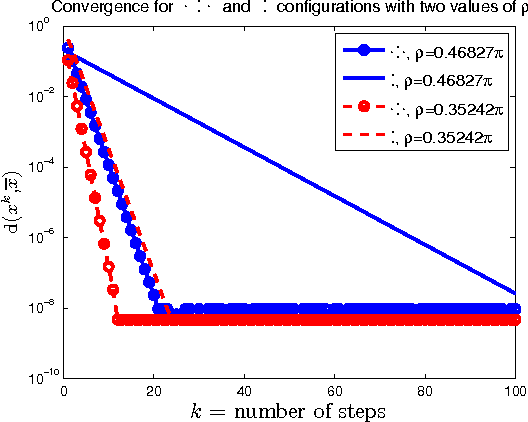
We study the problem of finding the global Riemannian center of mass of a set of data points on a Riemannian manifold. Specifically, we investigate the convergence of constant step-size gradient descent algorithms for solving this problem. The challenge is that often the underlying cost function is neither globally differentiable nor convex, and despite this one would like to have guaranteed convergence to the global minimizer. After some necessary preparations we state a conjecture which we argue is the best (in a sense described) convergence condition one can hope for. The conjecture specifies conditions on the spread of the data points, step-size range, and the location of the initial condition (i.e., the region of convergence) of the algorithm. These conditions depend on the topology and the curvature of the manifold and can be conveniently described in terms of the injectivity radius and the sectional curvatures of the manifold. For manifolds of constant nonnegative curvature (e.g., the sphere and the rotation group in $\mathbb{R}^{3}$) we show that the conjecture holds true (we do this by proving and using a comparison theorem which seems to be of a different nature from the standard comparison theorems in Riemannian geometry). For manifolds of arbitrary curvature we prove convergence results which are weaker than the conjectured one (but still superior over the available results). We also briefly study the effect of the configuration of the data points on the speed of convergence.