On the Convergence of Approximate and Regularized Policy Iteration Schemes
Paper and Code
Oct 14, 2019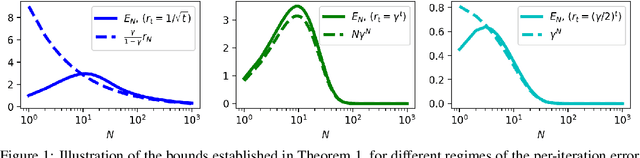
Entropy regularized algorithms such as Soft Q-learning and Soft Actor-Critic, recently showed state-of-the-art performance on a number of challenging reinforcement learning (RL) tasks. The regularized formulation modifies the standard RL objective and thus generally converges to a policy different from the optimal greedy policy of the original RL problem. Practically, it is important to control the sub-optimality of the regularized optimal policy. In this paper, we establish sufficient conditions for convergence of a large class of regularized dynamic programming algorithms, unified under regularized modified policy iteration (MPI) and conservative value iteration (VI) schemes. We provide explicit convergence rates to the optimality depending on the decrease rate of the regularization parameter. Our experiments show that the empirical error closely follows the established theoretical convergence rates. In addition to optimality, we demonstrate two desirable behaviours of the regularized algorithms even in the absence of approximations: robustness to stochasticity of environment and safety of trajectories induced by the policy iterates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge