On the boosting ability of top-down decision tree learning algorithm for multiclass classification
Paper and Code
May 17, 2016

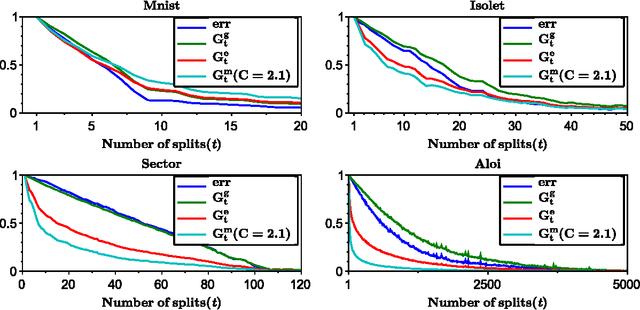
We analyze the performance of the top-down multiclass classification algorithm for decision tree learning called LOMtree, recently proposed in the literature Choromanska and Langford (2014) for solving efficiently classification problems with very large number of classes. The algorithm online optimizes the objective function which simultaneously controls the depth of the tree and its statistical accuracy. We prove important properties of this objective and explore its connection to three well-known entropy-based decision tree objectives, i.e. Shannon entropy, Gini-entropy and its modified version, for which instead online optimization schemes were not yet developed. We show, via boosting-type guarantees, that maximizing the considered objective leads also to the reduction of all of these entropy-based objectives. The bounds we obtain critically depend on the strong-concavity properties of the entropy-based criteria, where the mildest dependence on the number of classes (only logarithmic) corresponds to the Shannon entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge