On the approximation of rough functions with deep neural networks
Paper and Code
Dec 13, 2019
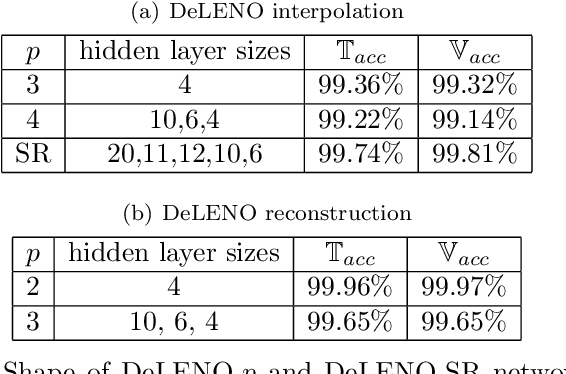


Deep neural networks and the ENO procedure are both efficient frameworks for approximating rough functions. We prove that at any order, the ENO interpolation procedure can be cast as a deep ReLU neural network. This surprising fact enables the transfer of several desirable properties of the ENO procedure to deep neural networks, including its high-order accuracy at approximating Lipschitz functions. Numerical tests for the resulting neural networks show excellent performance for approximating solutions of nonlinear conservation laws and at data compression.
* 30 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge