On the Achievable Rate of IRS-Assisted Multigroup Multicast Systems
Paper and Code
Aug 15, 2022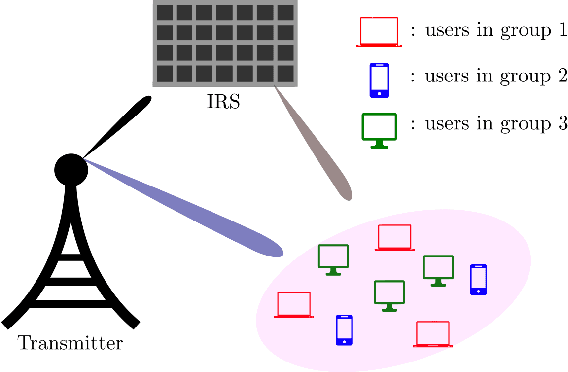
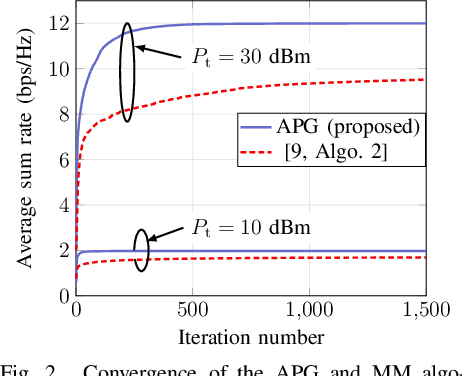
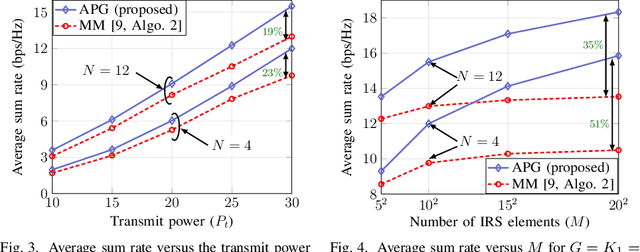
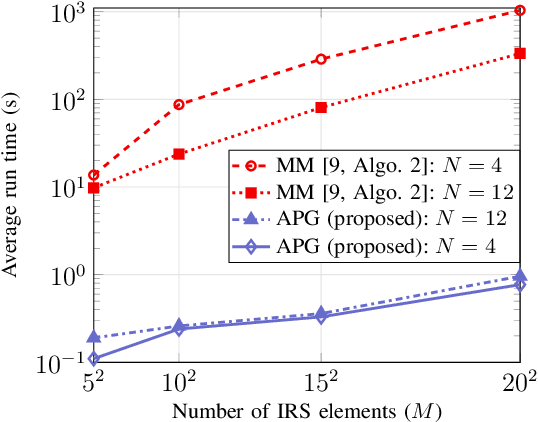
Intelligent reflecting surfaces (IRSs) have shown huge advantages in many potential use cases and thus have been considered a promising candidate for next-generation wireless systems. In this paper, we consider an IRS-assisted multigroup multicast (IRS-MGMC) system in a multiple-input single-output (MISO) scenario, for which the related existing literature is rather limited. In particular, we aim to jointly design the transmit beamformers and IRS phase shifts to maximize the sum rate of the system under consideration. In order to obtain a numerically efficient solution to the formulated non-convex optimization problem, we propose an alternating projected gradient (APG) method where each iteration admits a closed-form and is shown to be superior to a known solution that is derived from the majorization-minimization (MM) method in terms of both achievable sum rate and required complexity, i.e., run time. In particular, we show that the complexity of the proposed APG method grows linearly with the number of IRS tiles, while that of the known solution in comparison grows with the third power of the number of IRS tiles. The numerical results reported in this paper extend our understanding on the achievable rates of large-scale IRS-assisted multigroup multicast systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge