On Relative Pose Recovery for Multi-Camera Systems
Paper and Code
Feb 24, 2021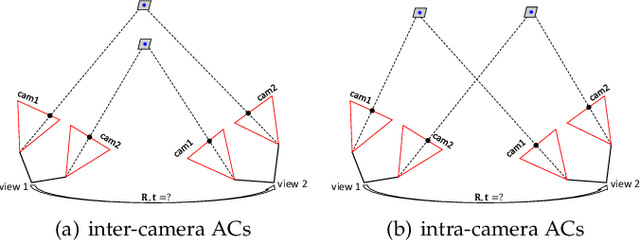
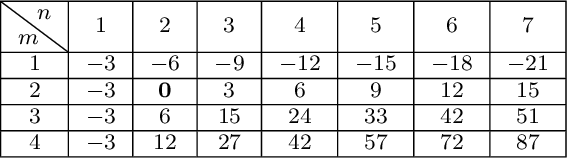
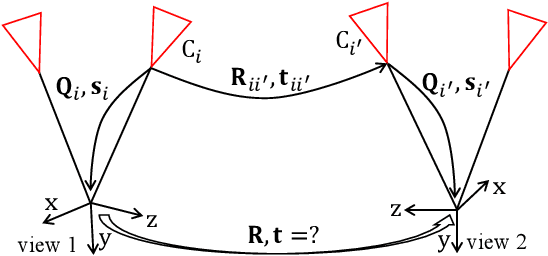
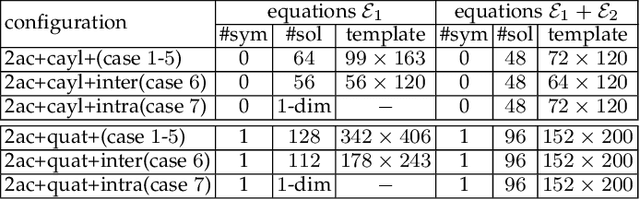
The point correspondence (PC) and affine correspondence (AC) are widely used for relative pose estimation. An AC consists of a PC across two views and an affine transformation between the small patches around this PC. Previous work demonstrates that one AC generally provides three independent constraints for relative pose estimation. For multi-camera systems, there is still not any AC-based minimal solver for general relative pose estimation. To deal with this problem, we propose a complete solution to relative pose estimation from two ACs for multi-camera systems, consisting of a series of minimal solvers. The solver generation in our solution is based on Cayley or quaternion parameterization for rotation and hidden variable technique to eliminate translation. This solver generation method is also naturally applied to relative pose estimation from PCs, resulting in a new six-point method for multi-camera systems. A few extensions are made, including relative pose estimation with known rotation angle and/or with unknown focal lengths. Extensive experiments demonstrate that the proposed AC-based solvers and PC-based solvers are effective and efficient on synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge