On Regularized Sparse Logistic Regression
Paper and Code
Sep 12, 2023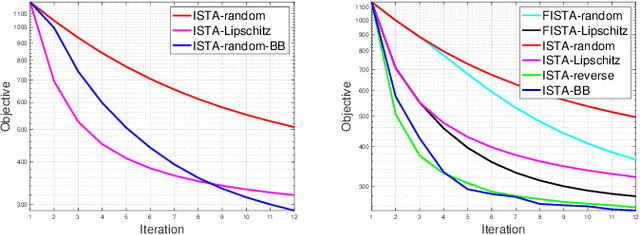
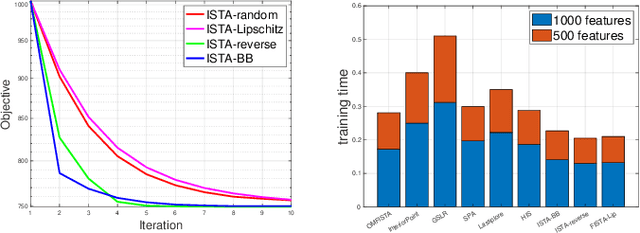
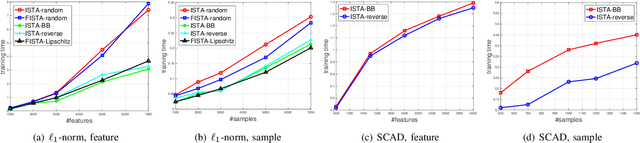
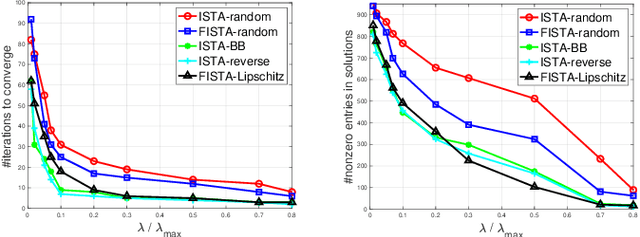
Sparse logistic regression aims to perform classification and feature selection simultaneously for high-dimensional data. Although many studies have been done to solve $\ell_1$-regularized logistic regression, there is no equivalently abundant literature about solving sparse logistic regression associated with nonconvex penalties. In this paper, we propose to solve $\ell_1$-regularized sparse logistic regression and some nonconvex penalties-regularized sparse logistic regression, when the nonconvex penalties satisfy some prerequisites, with similar optimization frameworks. In the proposed optimization frameworks, we utilize different line search criteria to guarantee good convergence performance for different regularization terms. Empirical experiments on binary classification tasks with real-world datasets demonstrate our proposed algorithms are capable of performing classification and feature selection effectively with a lower computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge