On Recursive Edit Distance Kernels with Application to Time Series Classification
Paper and Code
May 26, 2014
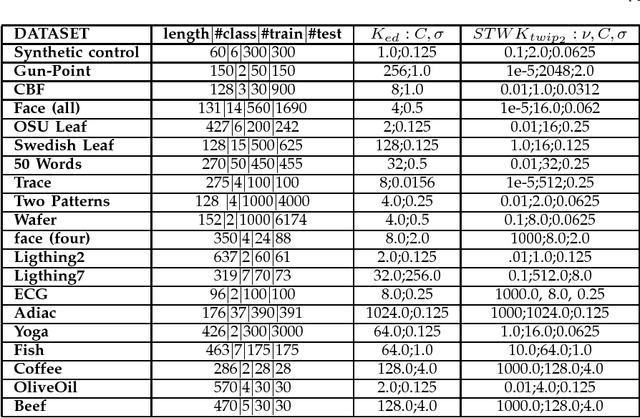
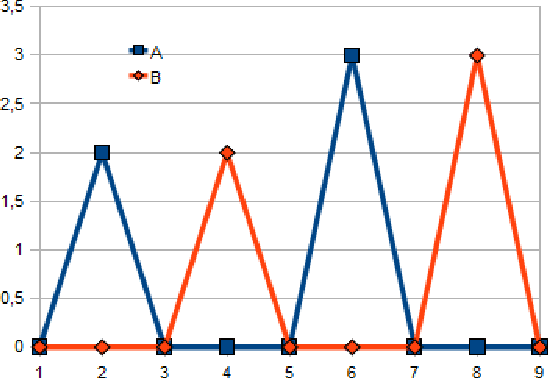
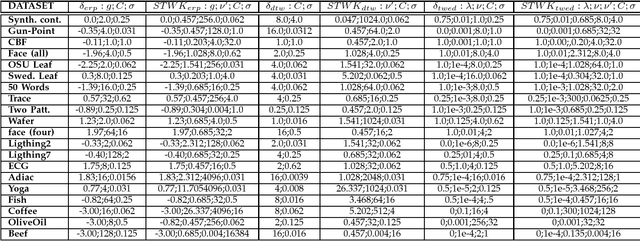
This paper proposes some extensions to the work on kernels dedicated to string or time series global alignment based on the aggregation of scores obtained by local alignments. The extensions we propose allow to construct, from classical recursive definition of elastic distances, recursive edit distance (or time-warp) kernels that are positive definite if some sufficient conditions are satisfied. The sufficient conditions we end-up with are original and weaker than those proposed in earlier works, although a recursive regularizing term is required to get the proof of the positive definiteness as a direct consequence of the Haussler's convolution theorem. The classification experiment we conducted on three classical time warp distances (two of which being metrics), using Support Vector Machine classifier, leads to conclude that, when the pairwise distance matrix obtained from the training data is \textit{far} from definiteness, the positive definite recursive elastic kernels outperform in general the distance substituting kernels for the classical elastic distances we have tested.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge