On Neural Learnability of Chaotic Dynamics

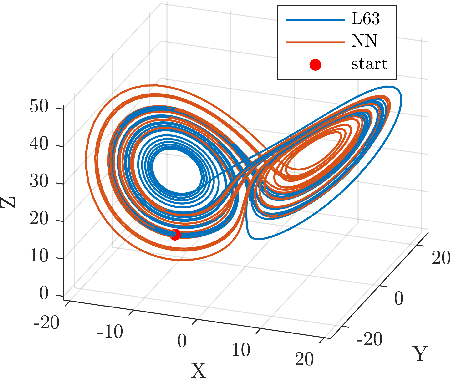
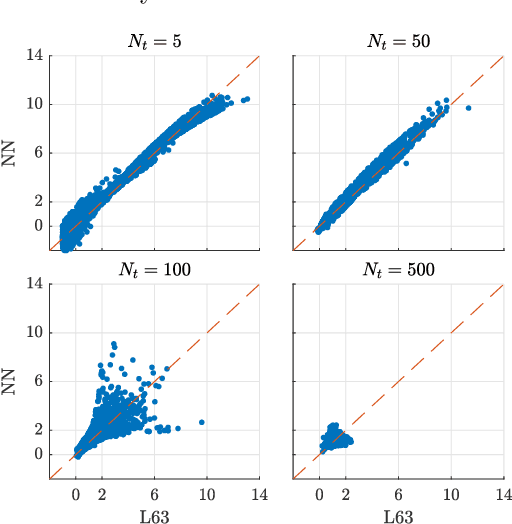
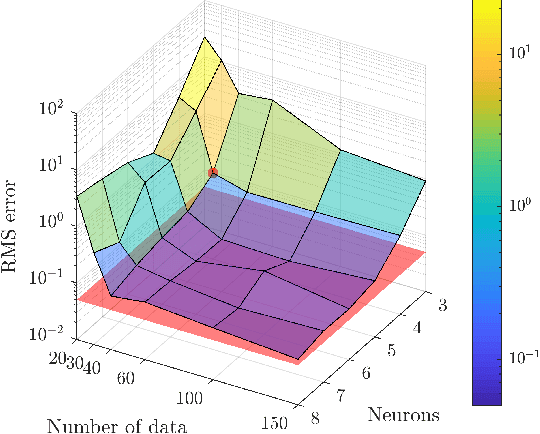
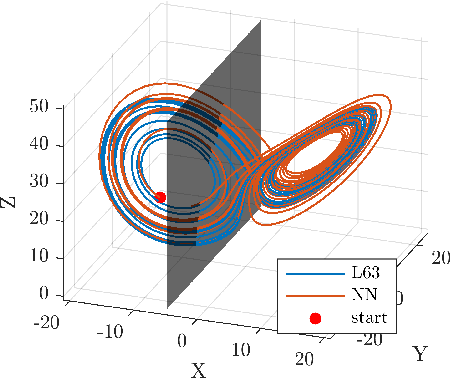
Neural networks are of interest for prediction and uncertainty quantification of nonlinear dynamics. The learnability of chaotic dynamics by neural models, however, remains poorly understood. In this paper, we show that a parsimonious feed-forward network trained on a few data points suffices for accurate prediction of local divergence rates on the whole attractor of the Lorenz 63 system. We show that the neural mappings consist of a series of geometric stretching and compressing operations that indicate topological mixing and, therefore, chaos. Thus, chaotic dynamics is learnable. The emergence of topological mixing within the neural system demands a parsimonious neural structure. We synthesize parsimonious structure using an approach that matches the spectrum of learning dynamics with that of a polynomial regression machine derived from the polynomial Lorenz equations.