On Minimizing Symbol Error Rate Over Fading Channels with Low-Resolution Quantization
Paper and Code
Jun 22, 2021
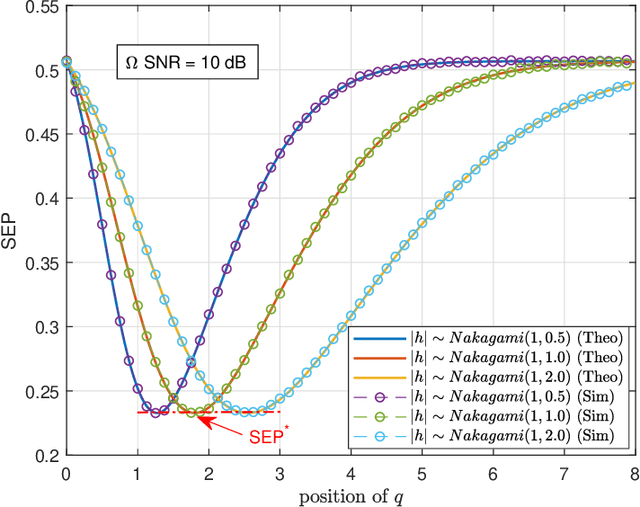
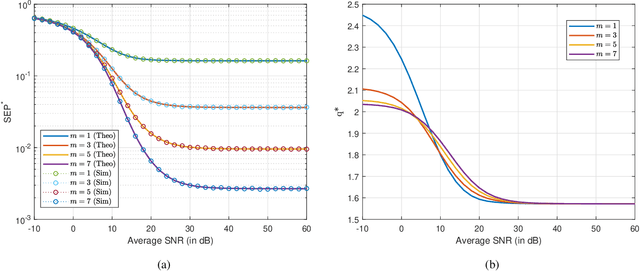
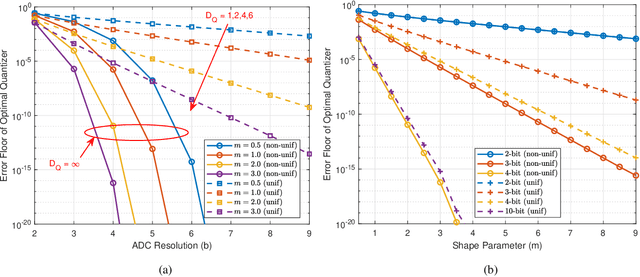
We analyze the symbol error probability (SEP) of $M$-ary pulse amplitude modulation ($M$-PAM) receivers equipped with optimal low-resolution quantizers. We first show that the optimum detector can be reduced to a simple decision rule. Using this simplification, an exact SEP expression for quantized $M$-PAM receivers is obtained when Nakagami-$m$ fading channel is considered. The derived expression enables the optimization of the quantizer and/or constellation under the minimum SEP criterion. Our analysis of optimal quantization for equidistant $M$-PAM receiver reveals the existence of error floor which decays at a double exponential rate with increasing quantization bits, $b$. Moreover, by also allowing the transmitter to optimize the constellation based on the statistics of the fading channel, we prove that the error floor can be eliminated but at a lower decay exponent than the unquantized case. Characterization of this decay exponent is provided in this paper. We also expose the outage performance limitations of SEP-optimal uniform quantizers. To be more precise, its decay exponent does not improve with $b$. Lastly, we demonstrate that the decay exponent of a quantized receiver can be complemented by receive antenna diversity techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge